Nota Técnica
|
|
| Aplicativo GAMMA-GUI: uma interface gráfica amigável para análise exploratória de dados no MATLAB GAMMA-GUI APP: a user-friendly graphical interface for exploratory data analysis in MATLAB |
|
Diego GalvanI,*,# I. Departamento de Química, Universidade Federal de Santa Catarina (UFSC), 88040-900 Florianópolis - SC, Brasil Recebido: 19/05/2025 *e-mail: diego.galvan@ufsc.br; ebona@utfpr.edu.br In this work, we continue our series of tutorial articles published in the Química Nova exploring different features of the GAMMA-GUI app (Grupo de Análise Multivariada em Matrizes Alimentares), a user-friendly interface for the multivariate analysis in Matlab®. This time, we demonstrate five types of exploratory data analysis (unsupervised learning), complemented by video demonstrations on our YouTube channel. Applications consist of demonstration with: (i) principal component analysis (PCA); (ii) self-organizing maps (SOM); (iii) hierarchical cluster analysis (HCA); (iv) k-means, and (v) common dimensions analysis (ComDim). Additionally, a demonstration of descriptive statistics with Tukey HSD (honest significant difference) has been included in this tutorial. Suggestions for improvements or new ideas for the app are welcome and can be directed to the developers. INTRODUÇÃO A quimiometria é a ciência que relaciona medidas feitas em um sistema ou processo químico, utilizando métodos matemáticos e estatísticos.1 As principais categorias da quimiometria incluem técnicas de planejamento de experimentos e de análise exploratória de dados, classificação e calibração multivariadas.2 Essas subdivisões representam abordagens distintas para lidar com experimentos e conjuntos de dados complexos de origem química, sendo fundamentais para a extração de características, classificações e calibrações em contextos multivariados. Outra subdivisão relevante no campo do aprendizado de máquina (machine learning) diz respeito à forma como os algoritmos processam os dados, os aprendizados supervisionados (supervised learning) e não supervisionados (unsupervised learning).3,4 Os não supervisionados não requerem conhecimento prévio sobre as saídas dos dados durante a fase de aprendizagem, ou seja, os dados não são rotulados, não possuem saídas pré-definidas nem variáveis-alvo. Já os supervisionados exigem a disponibilidade prévia (a priori) de informações qualitativa (para classificação) ou quantitativa (para calibração) para a construção dos modelos. Isso significa que os dados de treinamento são rotulados, com uma saída pré-definida ou variáveis-alvo. Em um problema de reconhecimento de padrões supervisionado, os preditores qualitativos ou quantitativos podem ser "aprendidos" de modo direcionado à resposta de interesse, enquanto em um problema não supervisionado os comportamentos são "aprendidos" de acordo com a similaridade das amostras disponíveis.4 O aprendizado não supervisionado é amplamente utilizado para fins exploratórios, para identificar tendências, semelhanças e diferenças entre amostras, reduzir a dimensionalidade dos dados e/ou extraindo padrões dominantes em matrizes de dados complexas, podendo ainda ser dividido entre análise exploratória de dados (exploratory data analysis, EDA) e agrupamento (clustering).5,6 A principal distinção reside no fato que, nos EDA, a ênfase recai sobre a compreensão intrínseca dos dados, destacando-se pela sua capacidade de revelar padrões sem a necessidade de formar grupos predefinidos, enquanto as técnicas de agrupamentos têm como finalidade agrupar as amostras com base em critérios específicos. Para o tratamento de dados de natureza química, destacam-se, devido a simplicidade, eficácia e robustez que proporcionam, a análise de componentes principais (principal component analysis, PCA), os mapas auto-organizáveis (self-organizing maps, SOM), a análise por agrupamento hierárquicos (hierarchical cluster analysis, HCA), o k-médias (k-means) e a análise por dimensões comuns (common dimensionanalysis, ComDim). Embora não exista uma distinção clara entre quimiometria e aprendizado de máquina, adotaremos a definição proposta por Santos et al.7 A quimiometria refere-se a abordagens baseadas em projeções, como a análise de componentes principais e fatorial, enquanto o aprendizado de máquina abrange um conjunto de algoritmos avançados que aprendem com os dados, direcionados à modelagem não linear e de alta complexidade. Essa distinção também reflete nas ferramentas utilizadas. Na emergente área de Ciência de Dados, cientistas de dados tendem a adotar linguagens como Python e uso de aprendizado de máquina. Por outro lado, quimiometristas ou cientistas de dados químicos, tradicionalmente vinculados à já consolidada Comunidade de Quimiometria, utilizam predominantemente o Matlab (MathWorks), como pode ser comprovado por meio de várias interfaces gráficas disponíveis gratuitamente como "MVC1",8 "MVC2",9 "MVC3",10 "DD-SIMCA",11 "PLS-DA",12 "MCR-ALS_GUI",13 etc., e comercialmente o "PLS_Toolbox". Alguns aplicativos em português já foram desenvolvidos para análise multivariada de dados, como o "ChemoStat",14 o "REDGIM®"15 e o "Photometrix".16 Embora sejam aplicativos bastante úteis, eles possuem algumas limitações, estando restritos somente à PCA, HCA e PLS (partial least squares). Além disso, o REDGIM® e o Photometrix foram especificamente projetados para a análise de imagens digitais, o que pode limitar sua aplicação para outros tipos de dados. No aplicativo GAMMA-GUI (Grupo de Análise Multivariada em Matrizes Alimentares), há uma série de interfaces e algoritmos direcionadas a técnicas de planejamento de experimentos e de análise exploratória de dados, classificação e calibração multivariadas, todos reunidos em uma única plataforma. Além disso, o GAMMA-GUI foi desenvolvido para ser flexível e não restrito a um único tipo de dado, ampliando suas possibilidades de aplicação. Em nosso primeiro tutorial com o aplicativo GAMMA-GUI, publicado na Química Nova,17 abordamos as técnicas de planejamento de experimentos (design of experiments, DoE). O GAMMA-GUI consiste em uma interface gráfica e amigável, desenvolvida em GUI (graphical user interface, GUI) e implementado usando programação orientada a objetos (object-oriented programming, OOP) do software Matlab®. O aplicativo permite que usuários novatos e experientes realizem tarefas de forma eficaz e eficiente, embora ainda seja necessário que os usuários tenham conhecimentos prévios de quimiometria. Além disso, a interface do aplicativo encontra-se em português-BR, conta com vídeos tutoriais demonstrativos no YouTube®18 e pode ser baixada gratuitamente no File Exchange - MATLAB Central19 ou no GitHub®.20 Dando continuidade à nossa série de artigos tutoriais, neste guia exploraremos a interface dedicada ao aprendizado não supervisionado, utilizando dados reais da literatura.
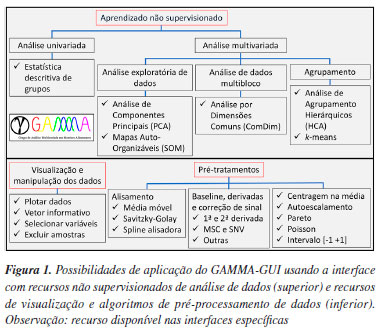
RECURSOS INTEGRADOS NA INTERFACE DE ANÁLISE EXPLORATÓRIA Os recursos de análise integrados na interface "Análise exploratória" do aplicativo GAMMA-GUI podem ser visualizados na Figura 1. Nesta interface, os usuários têm acesso à PCA, SOM, ComDim, HCA e k-means, além de funcionalidades para análise estatística descritiva de grupos. Adicionalmente, os usuários contam com recursos de visualização e pré-tratamentos de dados na interface "Visualização e pré-tratamentos".
Antes de iniciarmos, faremos um resumo da nomenclatura adotada neste tutorial. É fundamental esclarecer a nomenclatura usual referente à "técnica analítica", "método analítico", "modelo" e "algoritmo". As definições adotadas seguem, em grande parte, aquelas sugeridas por Mazivila e Olivieri.21 "Técnica analítica" refere-se a um procedimento instrumental utilizado para determinar a concentração de um analito. "Método analítico" é a aplicação específica de uma técnica a uma determinada amostra, sob condições definidas de medição. "Modelo" consiste em uma representação matemática que descreve as propriedades dos dados. "Algoritmo" é um conjunto detalhado de instruções destinado à execução de uma tarefa computacional. Como exemplo técnico, a PCA é um modelo quimiométrico, enquanto o SOM é um modelo de aprendizagem. Os filtros SNV (standard normal variate) e MSC (multiplicative scatter correction) são algoritmos utilizados para o pré-processamento de dados. A espectroscopia no infravermelho próximo (NIR) é uma técnica analítica. Já o método analítico pode ser entendido como a combinação de uma técnica analítica, como a espectroscopia NIR, com uma abordagem baseada em dados, como um modelo quimiométrico ou de aprendizagem. Além disso, são apresentados alguns conceitos fundamentais de álgebra linear e análise de dados essenciais para iniciantes. Entretanto, esse texto é apenas um breve guia para os usuários, discussões mais aprofundadas e sistemáticas podem ser encontradas nas obras específicas.1,3,6,22
A seguir, fornecemos uma breve fundamentação teórica dedicada aos recursos de aprendizagem não supervisionada mais utilizados na química que podem ser encontrados no aplicativo GAMMA-GUI. Análise de componentes principais (PCA) A PCA é um modelo quimiométrico baseado em projeção, amplamente utilizado para a redução da dimensionalidade de dados multivariados. Considerada a principal técnica de EDA, a PCA realiza uma transformação da base do espaço das variáveis originais, de dimensão RJ, para um novo espaço RA formado pelas A componentes principais utilizadas (PC). Essas componentes, também conhecidas como fatores, são definidas pelos autovetores da matriz de covariância/correlação que fornecem as direções das componentes principais no espaço RA e são determinadas de forma a maximizar a variância extraída dos dados. Cada PC possui um autovalor, que representa a quantidade de variância explicada por essa componente. As PCs são ordenadas em ordem decrescente de variância explicada, conforme indicado por seus autovalores. Ou seja, a primeira componente retém a maior parte da variabilidade dos dados, seguida pelas demais em ordem de importância, sendo que os autovalores diminuem progressivamente. Essa transformação de um conjunto original de variáveis inicialmente correlacionadas entre si, para um conjunto de variáveis não correlacionáveis entre si, é chamado de "compressão" devido a redução da dimensionalidade do conjunto de dados.1,3,6,22 O ponto de partida da PCA consiste na definição da matriz de dados X, que é constituída por I linhas (amostras) e J colunas (variáveis).
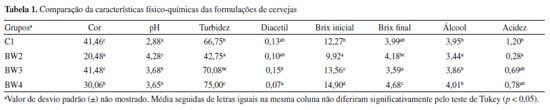
A decomposição dessa matriz 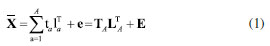 A matriz de escores T contêm as coordenadas de cada amostra em relação aos eixos das PCs, enquanto a matriz de pesos L contém a informação de quanto cada variável original contribuiu na formação de cada PC.3 O processo de decomposição da matriz pode ser realizado de diferentes formas, sendo a decomposição por valores singulares (singular value decomposition, SVD) a mais frequente devido à sua melhor performance para grandes conjuntos de dados com muitas variáveis. Entretanto, outra abordagem comum para calcular as matrizes de escores e de pesos é através do algoritmo NIPALS (nonlinear iterative partial least squares). Mais detalhes a respeito da decomposição SVD e NIPALS é dada por Ferreira.3 Uma descrição mais abrangente e clássica da PCA é apresentada por Bro e Smilde,25 enquanto Rodionova et al.26 discutem as novas ferramentas e tendências recentemente associadas ao modelo PCA. Mapas auto-organizáveis (SOM) O SOM é modelo de aprendizagem não linear para análise exploratória de dados complementar à PCA, introduzido por Teuvo Kohonen na década de 1980.27 Quando o uso de modelos quimiométricos lineares, como a PCA, não for muito informativo devido a uma estrutura de dados complexa, abordagens não lineares podem permitir uma melhor compreensão dos dados.1 Como o nome sugere, no SOM os dados são organizados de modo não supervisionado em um "mapa" tipicamente bidimensional, semelhante, ao gráfico de escores da PCA. O SOM é considerado uma rede neural competitiva do tipo feed-forward de camada única, inspirada no cérebro humano, e seu fundamento consiste em nós de entrada e uma grade de nós computacionais conectados (neurônios) que competem entre si para serem "ativados". Durante o treinamento da rede neural, o neurônio i com a menor distância Euclidiana D (Equação 2) entre o vetor de entrada x e o vetor de pesos do neurônio w é chamado de "neurônio vencedor" ou best matching unit (BMU).1,6,27,28 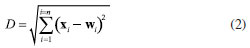 Durante a etapa de cooperação os vetores modelos nas proximidades do BMU vão cooperar para formar uma região do SOM especializada em padrões similares ao da amostra x. Em seguida, ocorre o processo de atualização dos pesos dos neurônios vizinhos ao BMU seguindo o postulado de aprendizagem de Hebb (Equação 3). 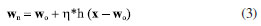 Sendo que wn representa o novo vetor de pesos do neurônio, wo o vetor de pesos do neurônio antes da atualização, η a taxa de aprendizado e h a função de vizinhança. O processo é repetido várias vezes até que os neurônios estejam organizados em um mapa topológico, onde neurônios próximos representam dados similares.1,6,27,28 Análise de agrupamentos hierárquicos (HCA) A HCA é um modelo quimiométrico não supervisionado de agrupamento "suave" (soft clustering), pois os objetos podem pertencer a múltiplos clusters em diferentes níveis de hierarquia, útil para redução da dimensionalidade de grandes conjuntos de dados. Inicialmente, ocorre um particionamento dos objetos em k = 1,..., n clusters, que posteriormente são ordenadas hierarquicamente pelo modo aglomerativo ou divisivo. A opção aglomerativa é a adotada no aplicativo, por meio da função "linkage" do Matlab.29 Nessa abordagem, o primeiro passo consiste em considerar cada objeto como um grupo unitário/único, e então, segue agrupando sistematicamente os grupos por ordem de similaridade. No caso da abordagem divisiva, inicia-se por grupos que vão se dividindo em subgrupos por dissimilaridade.3 Os clusters são formados entre amostras que tenham comportamento semelhante, cuja fundamentação consiste em maximizar a homogeneidade intragrupo e maximizar a heterogeneidade intergrupo. Uma maneira de determinar semelhanças entre as amostras, é feito através do conceito de métricas de distância entres eles, que podem ser obtidas de diferentes formas.1,3 No espaço multivariado RJ, a distância estimada entre dois objetos definidos pelos vetores xA (com componentes/variáveis xA1, xA2,..., xAj) e xB (com componentes/variáveis xB1, xB2,..., xBj) mais populares entre os químicos é a Euclidiana, Manhattan (cityblock) e Mahalanobis (Equações 4, 5 e 6), onde Var-1, é a inversa de matriz de variância-covariância que explica a dispersão dos dados ao redor do centroide. Para mais detalhes consultar Ferreira.3,30 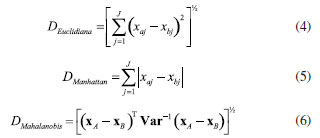 Existem ainda outras métricas de distância, entre elas, destacam-se a distância Euclidiana ao quadrado, Minkowski, Chebyshev, cosseno (cosine), correlação (correlation), Spearman, Hamming e Jaccard. Maiores detalhes sobre essas estimativas podem ser encontrados em Varmuza e Filzmoser 1 e ajuda do Matlab.31 A etapa seguinte consiste no "linkage", que calcula a distância entre os grupos de amostras durante a construção do dendrograma, que são obtidos utilizando índices de similaridade, que permitem identificar grupos de objetos com base em diferentes níveis de similaridade, onde o comprimento dos ramos reflete diretamente o grau de similaridade entre os grupos. Então, a distância entre dois clusters com índice l e m pode ser determinada de várias maneiras, sendo os mais utilizados o algoritmo do vizinho mais próximo (single), mais distante (complete), pela média (average), centroide e de Ward.1,3 Entretanto, outros algoritmos para calcular distância entre clusters pela mediana (median) e distância média ponderada (weighted) também podem ser utilizadas.29 O single forma agrupamentos esparsos, usando a menor distância entre elementos, sendo robusto a outliers. O complete, é baseado na maior distância, e produz clusters compactos, mas é sensível a outliers. O average equilibra ambos, calculando a média das distâncias, enquanto o weighted faz o mesmo, mas atribui pesos iguais aos clusters, independentemente do tamanho. O median usa a mediana das distâncias, sendo mais robusto que o centróide. Já o método do centróide agrupa clusters pela proximidade de seus centróides, mas pode gerar intercruzamentos no dendrograma. Por fim, o Ward minimiza a variância interna, criando grupos homogêneos e balanceados, porém com maior custo computacional. Todos, os "linkage" exceto single e complete, são interpretáveis via centróides ou médias.1,3,29 Agrupamento k-means O k-means é considerado um modelo de aprendizagem não supervisionado de agrupamento "rígido" (hard clustering), ou seja, cada ponto de dados no espaço n-dimensional pertence apenas a um cluster. As estimativas das distâncias entre pares de objetos, juntamente com a definição do número desejado de k-clusters, formam a base fundamental do k-means. Internamente, o algoritmo utiliza os chamados centroides (means), que representam o centro de cada cluster.1,28,32 Um centroide cj de um cluster j = 1,..., k, pode ser definido como o vetor da média aritmética de todos os objetos do cluster correspondente (Equação 7).  O k-means tem como objetivo minimizar a soma dos quadrados total dentro do cluster(Equação 8). 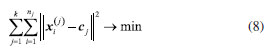 onde Análise por dimensões comuns (ComDim) O ComDim pertence à classe de análise de dados multibloco, cujo objetivo é extrair uma representação global de um conjunto comum de amostras, a partir de diferentes matrizes que contêm informações de naturezas distintas. A decomposição é descrita pela Equação 9.  onde Wk = XkXkT é a matriz de produtos cruzados associada à matriz de dados Xk, sendo k = 1, 2,...K, resultando em uma matriz quadrada de dimensão I × I, onde I é o número de amostras. Cada matriz Xk é inicialmente normalizada por sua norma de Frobenius, dada por As CDs são extraídas sequencialmente, empregando um algoritmo similar ao NIPALS, a partir da matriz WG (concatenação ponderada pela respectiva saliência de cada matriz Wk). As saliências são inicializadas com valores unitários e recalculadas em cada iteração do algoritmo até atingir o critério de convergência. Após a extração da primeira CD as matrizes individuais são deflacionadas e o processo é repetido para a extração das próximas CDs. A matriz WG pode ser decomposta de maneira não supervisionada de três distintas formas, empregando a decomposição em valores singulares (SVD), por análise de componentes independentes (independent components analysis, ICA) ou por análise de componentes comuns (common components analysis, CCA). Para mais detalhes consultar os trabalhos de Bouveresse e Rutledge,35 Mishra et al.,36 Cariou et al.37 e El Ghaziri et al.38 A cada CD extraída é obtido um conjunto de saliências, escores e pesos. A saliência representa o peso atribuído a cada bloco para a construção de uma dada CD, e pode ser interpretada como a variância do bloco representada naquela CD, os escores representam as projeções das amostras no espaço comum da CD, e os loadings os pesos das variáveis contidas em cada bloco, análoga a PCA.34,39 Um fator essencial a ser considerado antes da análise do ComDim, é que os conjuntos de dados ou blocos gerados com diferentes técnicas analíticas (como espectroscópicos, cromatográficos, eletroanalíticos, entre outros) devem ser provenientes das mesmas I amostras. Em outras palavras, as matrizes podem ter diferentes tamanhos para as J colunas (variáveis), mas precisam ter o mesmo número de I linhas (amostras). Além disso, é fundamental observar que as amostras devem estar organizadas na mesma ordem em cada matriz Xk antes da análise dos dados.34 Estatística descritiva univariada Frequentemente, nos deparamos com a necessidade de realizar comparações entre duas ou mais médias populacionais. Nestes casos a realização de múltiplos testes t não é apropriada para avaliar a significância das diferenças entre as médias de pares de grupos, pois a probabilidade de um erro Tipo I aumenta com o número de comparações entre grupos. Portanto, testes para múltiplas comparações de grupos, como a análise de variância (analysis of variance, ANOVA), são mais apropriados, desde que o conjunto de dados atenda aos critérios, como distribuição normal dos resíduos e homogeneidade de variância, que podem ser verificadas pelos testes de Shapiro-Wilk ou Levene, respectivamente. A principal desvantagem da ANOVA consiste na falta de identificação de quais grupos específicos diferem entre si, ou ainda na dificuldade de verificar quais são estatisticamente iguais ou diferentes. Neste caso, uma abordagem muito útil que possibilita julgar se as médias são iguais ou não, e que é amplamente utilizada, é o teste de Tukey HSD (do inglês: honest significant difference).40 O HSD de Tukey é um teste post-hoc comumente utilizado após a realização da ANOVA e é muito útil para verificar diferenças significativas entre as médias de três ou mais grupos em uma série de experimentos químicos.
INTERFACE GRÁFICA Neste segundo tutorial, serão realizadas aplicações práticas utilizando outras interfaces do aplicativo GAMMA-GUI. O aplicativo, juntamente com os conjuntos de dados usados como demonstração neste tutorial, está disponível para download no GitHub20 ou no file Exchange da MathWorks.19 Para a instalação do GAMMA-GUI utilizando a opção do GitHub, os usuários devem consultar as instruções no nosso primeiro tutorial.17 A instalação utilizando a versão do File Exchange é mais simples e pode ser realizada diretamente no Matlab. Para isso, basta que os usuários abram o arquivo executável baixado do site do file Exchange. Após o processo de instalação, o aplicativo pode ser executado ao apertar o botão "GAMMA" na aba "APPS" do Matlab, conforme o vídeo de instalação.41 O aplicativo foi testado nas versões do software Matlab R2022a a R2024a. Para sua íntegra utilização, requer funções dos toolboxes "Global Optimization Toolbox", "Optimization Toolbox", "Statistics Machine Learning Toolbox", "Bioinformatics Toolbox" e "Signal Processing Toolbox". Para usuários que não têm acesso à licença do Matlab, alguns recursos do aplicativo GAMMA-GUI podem ser utilizados através da versão online do Matlab (observação: nessa modalidade, o uso é restrito ao ambiente online, com um limite de 20 h mensais de utilização). O processo começa com a criação de uma conta no site da MathWorks42 utilizando um e-mail institucional. Em seguida, basta fazer o download e a instalação do aplicativo através da aba "APPS" no Matlab Online, conforme as instruções detalhadas disponíveis em nosso Instagram.43 Conhecendo as interfaces do GAMMA-GUI Na interface "Visualização e pré-tratamentos", os usuários têm a possibilidade de realizar a visualização, manipulação e pré-tratamento de dados (Figura 1Sa, Material Suplementar). Nessa interface, os usuários podem plotar os dados, selecionar variáveis, excluir amostras ou ainda aplicar diferentes algoritmos de pré-processamentos nos dados. Existem diversas opções de algoritmos disponíveis na literatura, e no GAMMA-GUI os usuários têm as principais metodologias para análise multivariada, entre elas o alisamento pela média móvel, com filtro de Savitsky-Golay e Spline alisadora, técnicas de derivadas, correção de sinal MSC (multiplicative scatter correction) e SNV (standard normal variate), correção de linha de base e interpolação. Enquanto na interface "Análise Exploratória", os usuários têm a possibilidade de utilizar diferentes estratégias não supervisionadas de análises de dados, tais como HCA, PCA, SOM, k-means e ComDim (Figura 1Sb, Material Suplementar).
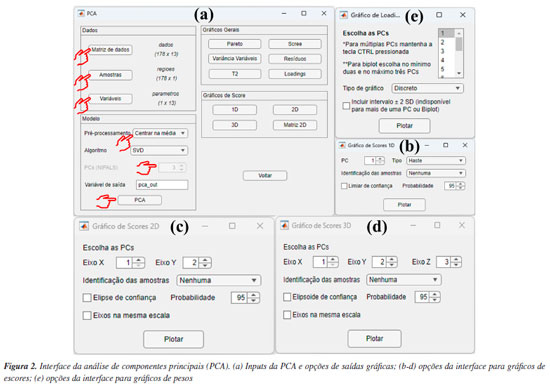
DEMONSTRAÇÕES USANDO O GAMMA-GUI Neste segundo artigo tutorial, concentramos nossas demonstrações usando as interfaces "Análise Exploratória" e "Visualização e pré-tratamentos". Para isso, diferentes conjuntos de dados foram selecionados do banco de dados do Matlab, dos autores e da literatura para demonstrar as aplicabilidades e funcionalidades do aplicativo. Neste tutorial, fornecemos aos usuários um passo a passo dos procedimentos adequados que devem ser seguidos para a análise não supervisionada de dados, assim como a interpretação dos resultados obtidos, utilizando uma interface gráfica amigável e livre de programação. Cabe ainda salientar que recursos extras do uso do aplicativo podem ser encontrados em nosso canal no YouTube, através de vídeos tutorias.18 Ressaltamos também que a utilização do GAMMA-GUI por usuários iniciantes também é recomendada e fomentada pelos desenvolvedores do aplicativo, desde que os usuários busquem alguns conhecimentos prévios sobre o assunto antes da sua utilização. PCA Adiante, demonstramos passo a passo como realizar e interpretar os resultados da PCA. Entretanto, é fundamental que, antes da etapa de análise, os usuários organizem os dados da matriz X da seguinte maneira: as linhas devem ser compostas pelas amostras e as colunas pelas variáveis. Nesse exemplo demonstrativo, utilizamos um conjunto de dados que consiste em 13 parâmetros físico-químicos determinados de 178 amostras de vinhos de diferentes regiões vinícolas italianas denominadas: Barolo (O), Grignolino (G) e Barbera (E).44 A matriz X para esse conjunto de dados é dada por I linhas que correspondem às amostras de vinhos × J colunas correspondem aos parâmetros físico-químicos, gerando uma matriz com dimensões 178 × 13, disponível no material de demonstração "dados_vinho" e YouTube.45 Ao carregar o material de demonstração no Matlab, os usuários terão acesso a uma série de estruturas disponíveis no workspace, como a matriz "dados", que contém os valores dos parâmetros físico-químicos determinados nos vinhos; três vetores de caracteres "nomes", "regioes" e "parametros", que contêm, respectivamente, os nomes completos das regiões vinícolas, as regiões vinícolas abreviadas de cada amostra de vinho e os nomes dos parâmetros físico-químicos determinados. Nesta demonstração, optamos por abreviar os nomes das regiões vinícolas para facilitar a interpretação e a visualização nas saídas gráficas da PCA. Iniciaremos a análise abrindo a janela "Análise Exploratória" do GAMMA-GUI e apertando o botão "PCA". Após essa etapa, uma nova janela se abrirá, onde os usuários precisam definir os inputs para realizar a análise, selecionando a matriz de dados e os vetores que identificam as amostras e variáveis na interface do aplicativo, utilizando os botões "Matriz de dados", "Amostras" e "Variáveis", conforme mostrado na Figura 2a. Ao apertar cada um desses botões, uma nova janela "Selecione as variáveis" será aberta, e, em cada uma delas, os usuários precisam definir adequadamente a matriz de dados e os vetores que identificam as amostras e variáveis. Neste caso, após apertar o botão "Matriz de dados", a estrutura "dados" deve ser selecionada, no botão "Amostras" selecionar "regioes" e, em "Variáveis", selecionar "parametros", como ilustrado na Figura 2a. Cabe ainda salientar que os vetores que identificam as amostras e variáveis devem estar no formato "cell array", onde cada célula pode conter qualquer tipo de dado. Aqui, essas estruturas contêm as informações dos nomes abreviados das regiões vinícolas italianas, representadas pelo vetor "regioes", e nomes dos parâmetros físico-químicos (álcool, ácido málico, cinzas, alcalinidade das cinzas, magnésio, fenólicos totais, flavonoides, fenólicos não flavonoides, proantocianidinas, intensidade de cor, matriz de coloração "hue", oxigênio dissolvido e prolina), representados pelo vetor "parametros".
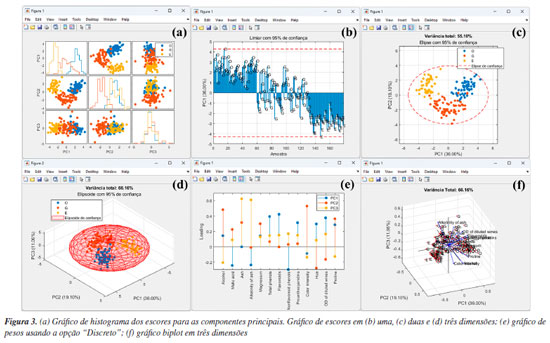
Na etapa seguinte, os usuários devem definir o tipo de pré-tratamento que será aplicado nas variáveis - colunas da matriz X usando o botão "Pré-processamento". Esse procedimento é essencial em qualquer análise quimiométrica, pois facilita a detecção e identificação de padrões e características relevantes nos conjuntos de dados químicos.1 Entre as opções de pré-tratamentos, o autoescalamento e a centragem na média estão entre os mais usuais. Neste exemplo, o autoescalamento é o procedimento mais recomendável, pois as variáveis têm diferentes unidades ou amplas faixas de variações. Nesses casos, ao aplicar esse procedimento, iguala-se o impacto entre as variáveis, ou seja, dá-se a mesma importância para todas as variáveis do conjunto de dados. Para a seleção do tipo de pré-tratamento no GAMMA-GUI, os usuários devem selecionar no botão "Pré-processamento", e escolher a opção "Autoescalamento". Agora, se o objetivo do usuário for avaliar dados espectrais, é preferível a aplicação da opção "Centragem na média", pois, ao centralizar os dados na média, a estrutura dos dados é preservada e a direção de maior dispersão ao redor dessa média coincide com a direção de maior variância interna dos dados, ou seja, as coordenadas são movidas para o centro dos dados, permitindo que as diferenças entre as variáveis se tornem mais perceptíveis.3,23,30 Existem ainda outras estratégias de pré-tratamentos, tais como o escalamento pela variância, pela amplitude, e variações de autoescalamento, como o autoescalamento de Pareto, VAST (variable stability) e nivelamento, entre outros.3 Além das etapas de pré-tratamento aplicadas às colunas da matriz X, existe ainda a possiblidade de pré-tratamento aplicado às linhas da matriz X, ou seja, às amostras que compõem o conjunto de dados. Estudos que envolvem dados espectrais, na maioria dos casos, requerem determinadas etapas de pré-processamento com o uso de algoritmos específicos. Frequentemente, estas etapas são aplicadas para minimização de informações indesejadas em dados espectroscópicos, como a correção do deslocamento da linha de base e fase/inclinação, correção de efeitos de espalhamentos em espectros de infravermelho próximo ou médio, ou variações em espectros de Raman e UV-Vis, ou ainda correções de deslocamentos em espectros de RMN ou cromatogramas desalinhados, entre outros tipos de correções existentes. Maiores detalhes podem encontrados na obra de Ferreira.3 Caso os usuários necessitem aplicar tais recursos em seus dados, na interface "Visualização e pré-tratamentos" do GAMMA-GUI (Figura 1Sa), os usuários têm a disponibilidade de escolher opções de alisamento, derivadas, correção de sinal, linha de base e interpolação de dados. Entretanto, se os usuários precisarem alinhar os dados no eixo das ordenas, como frequentemente é requerido em espectros de RMN ou cromatogramas, uma ótima ferramenta é o icoshift (interval-correlation-shifting),46 um algoritmo de código aberto para Matlab, disponibilizado para download em Chemometrics Research.47 A etapa seguinte consiste em definir o algoritmo e o número de componentes principais usando os botões "Algoritmo" e "PCs", respectivamente. No GAMMA-GUI, os usuários têm disponível as opções "SVD" (singular value decomposition) ou "NIPALS" (nonlinear iterative partial least squares) para o cálculo das matrizes de escores e de pesos. Neste exemplo, escolhemos o SVD, pois é considerada uma opção mais acurada e estável para cálculos das componentes principais. Para aplicações em que a matriz X possui muitas colunas e um posto químico pequeno (ou seja, alta correlação entre as variáveis), o NIPALS é recomendável, pois os vetores dos pesos e dos escores são calculados iterativamente, um de cada vez, o que reduz o tempo e esforço necessários para o processamento dos dados.3,23,30 O NIPALS é particularmente indicado para conjuntos de dados muito grandes, especialmente quando a análise é realizada em sistemas computacionais mais modestos, nos quais a decomposição SVD pode exigir uma quantidade elevada de memória. Para o algoritmo SVD, serão calculadas todas as PCs possíveis. Após a definição das etapas anteriores, é hora de realizar a análise, apertando o botão "PCA". Se os usuários desejarem, na caixa "Variável de saída", têm a liberdade de criar suas próprias nomenclaturas. Contudo, como default, a estrutura de saída dos dados é definida como "pca_out". Na estrutura de saída "pca_out" (default), os usuários têm à disposição uma série de recursos, como o acesso a matriz de escores "T", matriz de pesos "P", matriz de resíduos "Residuos", variância explicada "explained", teste de Hotelling's "T2" (mais informações sobre T2 são fornecidas adiante), entre outros. Os usuários também podem ainda gerar gráficos, acessando as opções "Gráficos Gerais" e "Gráficos de Score", ver Figura 2. Algumas opções de "Gráficos Gerais" estão ilustradas na Figura 2S (Material Suplementar), como o gráfico de "Pareto" (Figura 2Sa), "Scree" (Figura 2Sb), "Variância Variável" (Figura 2Sc) e "T2" (Figura 2Sd). Existe ainda, a opção de plotar o gráfico de resíduos, que não é demonstrado neste exemplo. A análise simultânea dos gráficos das Figuras 2Sa e 2Sb possibilita a definição do "posto químico" da matriz, ou seja, o número mínimo de novas variáveis capazes de descrever a máxima informação dos dados originais após a compressão. Essas novas variáveis são denominadas componentes principais, ou ainda fatores ou autovetores.3 De acordo com a Figura S2b, os autovalores apresentam uma redução significativa a partir de quatro a cinco PCs. Para este conjunto de dados, utilizamos também o conhecimento prévio do problema para determinar o número de A PCs a serem consideradas. Sabemos que há três origens geográficas distintas para os vinhos, o que nos permite, inicialmente, assumir que três PCs poderiam ser suficientes para diferenciar entre esses grupos, uma para cada região vinícola. É importante destacar, no entanto, que isso não significa que três PCs sejam suficientes para descrever toda a variabilidade do conjunto de dados. Elas podem, contudo, ser adequadas para a tarefa específica de diferenciar as amostras com base na região de origem, desde que carreguem informação relevante para essa distinção. Vale lembrar que as PCs são determinadas com base na maximização da variância dos dados, e não na separação entre classes. Portanto, a separação entre os três tipos de vinho nas três primeiras PCs só é possível porque as variáveis medidas contêm, de fato, informações discriminantes relacionadas à origem geográfica, enquanto as outras PCs descrevem outras informações que nos interessam no momento. Os valores de variâncias das PCs são cumulativos. Neste caso, a PC1 teve uma variância de 35,99%, PC2 de 19,09% e PC3 de 11,06%, totalizando uma variância de 66,15% da informação original dos dados, ver Figura 2Sa. Na Figura 2Sc, os usuários podem ainda verificar a contribuição de cada variável (neste caso, os parâmetros físico-químicos) em uma dada PC. Neste estudo, os flavonoides, fenóis totais e oxigênio dissolvido foram as variáveis/parâmetros que mais contribuíram na PC1, a intensidade de cor e teor de álcool na PC2, cinzas e alcalinidade das cinzas na PC3, e assim por diante. Em estudos com um número elevado de variáveis, como em dados espectrais, essa interpretação não é trivial. A matriz de resíduos E na PCA possibilita a estimativa de parâmetros estatísticos fundamentais para a análise dos dados. Na estrutura de saída "pca_out", ao acessar "Residuos", os usuários têm acesso a matriz de resíduos em "Res", o parâmetro "Q", que mede o quão bem cada amostra se ajusta ao novo subespaço definido pelas A PCs. Esse parâmetro é calculado pela soma quadrática dos elementos de cada linha da matriz E.3 Além disso, o "Xprev" é uma estimativa da matriz X nas A PCs definidas. Ao apertar o botão "Resíduos", os usuários podem facilmente verificar graficamente a distribuição dos resíduos das amostras para cada PC, gráfico não mostrado. Outro recurso fundamental é a possibilidade de detecção de amostras anômalas "outliers", isto é, identificar amostras que tenham comportamentos atípicos dentro do conjunto de dados. Existem várias estratégias estatísticas que viabilizam a identificação de amostras anômalas, no GAMMA-GUI as estimativas são obtidas usando o teste de Hotelling's (T2), que é uma extensão do teste t de Student para múltiplas variáveis. No GAMMA-GUI, a análise é baseada na estatística T2 de Hotelling, utilizando a distância de Mahalanobis como medida de cálculo. Essa distância é comparada a um limite crítico (α), sendo o valor resultante usado como critério para detectar amostras outliers no espaço da PCA, com base na estatística T2 calculada a partir da distribuição F. Embora a estatística T2 de Hotelling e a distância de Mahalanobis sejam conceitualmente distintas, elas tornam-se matematicamente equivalentes no contexto específico da PCA, quando os dados estão centrados na média, projetados em componentes principais ortogonais, e padronizados pela divisão pelas raízes quadradas dos respectivos autovalores (1/√λi). Essa equivalência numérica ocorre porque, neste espaço transformado, a matriz de covariância dos componentes principais padronizados se reduz exatamente à matriz identidade.1 O teste T2 mede o desvio de cada observação dentro do espaço PCA, e consiste em determinar as probabilidades de uma amostra pertencer a um grupo específico para um dado nível de confiança (α).6 Se o valor calculado da estatística T2 for maior que um valor crítico, sugere-se a presença de amostra outlier.1 Mais detalhes nos trabalhos de Varmuza e Filzmoser,1 Brereton6 e Gemperline.48 Apertando o botão "T2", ou ainda acessando a estrutura de saída de dados "T2" em "pca_out", os usuários podem evidenciar a existência de possíveis outliers considerando as primeiras A componentes principais para um dado nível de significância. De acordo com a Figura 2Sd, neste caso, é possível verificar cinco possíveis outliers com base na projeção no espaço PCA com as três primeiras PCs ao nível de 95% de confiança, uma amostra de vinho Barolo (O) e quatro Grignolino (G). Amostras anômalas podem ocorrer por diversas razões, e devem ser verificadas caso a caso pelo analista, que a posteriori deve tomar a decisão de excluí-la ou não do conjunto de dados. Caso o usuário almeje excluir uma amostra do conjunto de dados, o botão "Excluir amostras" na interface "Visualização e pré-tratamentos" pode ser utilizado. Os gráficos mais importantes para interpretação dos resultados da PCA são o gráfico de escores, que projeta as amostras no eixo das componentes principais, e o gráfico de pesos, que indica o quanto cada variável original contribuiu para a formação das componentes principais. Outro recurso interessante é o gráfico biplot, que combina os escores e os pesos, podendo ser gerado em duas ou três dimensões. Os gráficos da Figura 3 resumem os resultados deste estudo usando as três primeiras PCs.
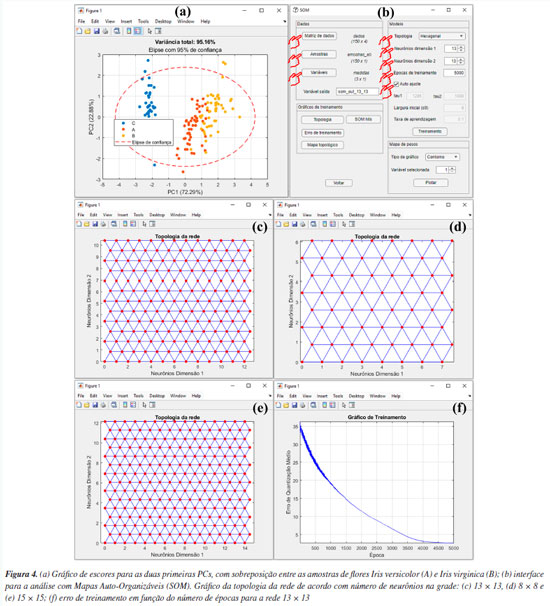
É recomendável iniciar a análise dos resultados da PCA através da análise dos gráficos de escores. Os usuários têm a possibilidade de gerar gráficos de escores em uma "1D", duas "2D" ou três dimensões "3D", ver Figuras 2b, 2c e 2d, ou ainda uma matriz de gráficos 2D com as possíveis combinações binárias das PCs escolhidas, ver Figura 3a. Os gráficos de escores são representações gráficas que indicam as projeções das amostras no novo sistema de coordenadas de dimensões reduzidas (PCs). Neste exemplo, nos limitamos à interpretação usando apenas as três primeiras componentes principais, conforme mostrado nas Figuras 3b-3d. No entanto, os usuários podem criar suas próprias combinações de gráficos de escores utilizando componentes principais de ordem superior. Durante a construção dos gráficos, os usuários podem ainda incluir os limiares de confiança para um nível de probabilidade α, marcando a caixa "Limiar de confiança", "Elipse de confiança" ou "Elipsoide de confiança" nos gráficos de uma, duas ou três dimensões, respectivamente. Nos gráficos de escores do GAMMA-GUI, os usuários podem optar por calcular limiares de confiança univariados baseados na distribuição F de Fisher: limites em 1D, elipses em 2D e elipsoides em 3D para cada PC, na PCA. Essa abordagem, de aplicação mais simples, permite verificar se os escores individuais estão dentro do intervalo esperado, considerando a variância explicada por cada PC avaliada. Além disso, é possível padronizar as escalas dos eixos nos gráficos de duas ou três dimensões marcando a caixa "Eixos na mesma escala", ou ainda escolher diferentes modos de identificação das amostras por cor, números ou nomes usando a caixa "Identificação das amostras". Na Figura 3b, é notável que a PC1 possibilitou diferenciar os vinhos Barolo (O) dos vinhos Barbera (E), enquanto os vinhos Grignolino (G) tem propriedades físico-química intermediárias entre os vinhos Barolo (O) e Barbera (E). Já a PC2 (gráfico 1D não mostrado) é fundamental para diferenciar os vinhos Grignolino (G) dos vinhos Barolo (O) e Barbera (E), sendo essa separação visível na Figura 3a. As Figuras 3c e 3d mostram os gráficos de escores para as duas e três primeiras PCs, respectivamente. Estes gráficos permitem uma melhor compreensão da diferenciação previamente relatada. Claramente evidencia-se a diferenciação entre os vinhos das diferentes regiões vinícolas italianas nas três primeiras PCs. Na opção "Loadings", o usuário pode plotar os gráficos de pesos de diferentes modos: "Discreto", "Linhas" ou "Biplot", conforme as opções na Figura 2e. A Figura 3e é uma representação da influência/pesos em termos da magnitude positiva ou negativa para uma variável em uma determinada componente principal. Neste caso, os pesos estão associados aos parâmetros físico-químicos avaliados. Para resumir, faremos uma discussão de apenas duas variáveis na PC1, porém, em uma análise real, é fundamental verificar e interpretar os resultados das demais PCs e de todas as variáveis. Tomando como exemplo os pesos de cada parâmetro na PC1, nota-se que os flavonoides apresentam o maior peso positivo, enquanto os compostos fenólicos não flavonoides tiveram o maior peso negativo. Ou seja, os teores de compostos fenólicos flavonoides e não flavonoides apresentam um maior peso para a diferenciação entre os vinhos de diferentes regiões vinícolas italianas na PC1. Associando a informação dos pesos ao gráfico de escores na PC1, é possível concluir que os vinhos Barolo (quadrante positivo da PC1) são mais ricos em compostos flavonoides, enquanto os vinhos Barbera (quadrante negativo da PC1) possuem um teor maior de fenólicos não flavonoides. Portanto, o sinal positivo ou negativo do peso, em conjunto com o sinal do escore, nos auxilia a identificar quais amostras têm um valor maior ou menor de uma determinada variável. Uma representação mais abrangente dos resultados da PCA é dada pelo gráfico biplot, que é uma representação conjunta dos pesos e escores em duas ou três dimensões. Na Figura 3f, temos o gráfico biplot para as três primeiras PCs. Neste caso, é notável a diferenciação entre os grupos de vinhos das diferentes regiões vinícolas italianas, sendo que a maioria dos vinhos Barbera (E) encontra-se no quadrante esquerdo do gráfico, os vinhos Barolo (O) no quadrante direito, e os vinhos Grignolino (G) no centro do gráfico. Tal diferenciação entre os vinhos deve-se fundamentalmente à influência, representada pelas linhas azuis na área do gráfico, que indicam os pesos de cada parâmetro, como teor de ácido málico e compostos fenólicos não flavonoides nas amostras de vinhos Barbera, flavonoides, fenóis totais e proantocianidinas nos vinhos Barolo, e matriz de coloração "hue" e oxigênio dissolvido nos vinhos Grignolino. SOM Neste exemplo, utilizamos o famoso conjunto de dados de flores Iris, publicado pelo estatístico e biólogo britânico Ronald Fisher.49 Este conjunto de dados é composto por 150 amostras, divididas igualmente entre três espécies: Irisversicolor (A), I. virginica (B) e I. setosa (C). Cada amostra teve quatro características taxonômicas medidas: comprimento da sépala, largura da sépala, comprimento da pétala e largura da pétala, em centímetros. A matriz de dados X para esse conjunto de dados é composta por I linhas (amostras de flores) e J colunas (características taxonômicas), resultando em uma matriz com dimensões 150 × 4, disponível no material de demonstração "dados_iris" e YouTube.50 Ao carregar o material de demonstração no Matlab, os usuários terão a matriz "dados", contendo os valores das medidas obtidas para todas as amostras, e três vetores de caracteres: "amostras", "amostras_ab" e "medidas", que correspondem, respectivamente, aos nomes das espécies botânicas de cada amostra, à nomenclatura abreviada criada para as amostras e às características taxonômicas medidas. Novamente, optamos por criar um vetor com os nomes abreviados para facilitar a interpretação e a visualização das saídas gráficas do SOM. Antes de iniciarmos a análise dos dados, precisamos esclarecer aos usuários alguns pontos fundamentais. O SOM é utilizado com uma finalidade semelhante à PCA; ambos permitem a redução da dimensionalidade do conjunto de dados, sendo que cada um apresenta suas vantagens e limitações. O SOM visa organizar dimensionalmente dados complexos, formando grupos de acordo com suas relações organizando-os em uma estrutura espacial chamada "mapa topológico", tradicionalmente uma grade bidimensional 2D. Enquanto na PCA não há nenhuma definição a priori da quantidade de dimensões (PCs) necessárias para representar os dados. Outra distinção fundamental entre ambos está na capacidade do SOM em lidar com conjuntos de dados caracterizados por comportamentos não lineares altamente complexos.24,28,51,52 Em outras palavras, o SOM pode capturar e representar melhor padrões complexos e não lineares presentes nos dados de forma mais fidedigna do que à PCA. Entretanto, o SOM requer conjuntos de dados substancialmente maiores, o que pode torná-lo mais suscetível ao overfitting quando aplicado em conjuntos de dados pequenos, ao contrário da PCA que não é susceptível a tais limitações. Outra desvantagem do SOM é o maior tempo computacional para análise dos dados e a necessidade de ajuste de uma quantidade maior de parâmetros do modelo, em comparação à PCA. Aconselhamos que os usuários priorizem abordagens mais simples, robustas e usuais como a PCA. Se tais abordagens não forem capazes de atender aos requisitos específicos ou de fornecer os resultados desejados, é recomendável que os usuários busquem considerar outras opções de análise de dados.4 Neste exemplo, iniciamos a análise do conjunto de dados de flores Iris seguindo as etapas descritas na seção anterior, utilizando à PCA, um modelo quimiométrico robusto, simples, de fácil implementação e com amplo potencial de aplicação. Em seguida, buscamos diferenciar as amostras utilizando um modelo de aprendizagem baseado em SOM, como uma alternativa complementar. Tradicionalmente, o conjunto de dados Fisher49 tem sido utilizado para propor novos algoritmos de aprendizado de máquina supervisionados, nos quais os modelos são construídos a partir de dados rotulados a priori. Seu uso para aprendizagem não supervisionados não é comum, uma vez que as amostras de Iris versicolor (A) e Iris virginica (B) não são facilmente separáveis usando esses modelos,52 conforme podemos visualizar nos resultados da PCA na Figura 4a. Em comparação, empregamos à análise discriminante linear (linear discriminant analysis, LDA), que possibilitou a classificação das três espécies de Iris com 100% de acurácia de predição. Entretanto, esses resultados não são explorados em profundidade neste tutorial, uma vez que o foco principal é a aprendizagem não supervisionada.
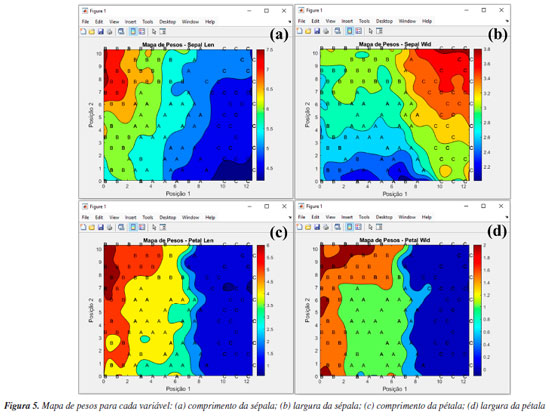
Para gerar o modelo de aprendizagem, aperte o botão "SOM" na janela "Análise Exploratória" do GAMMA-GUI. Após essa etapa, uma janela semelhante à Figura 4b se abrirá, e, nesta janela, os usuários precisam definir os inputs para realizar a análise, definindo a matriz de dados e os vetores que identificam as amostras e variáveis na interface do aplicativo, através dos botões "Matriz de dados", "Amostras" e "Variáveis", semelhante ao procedimento descrito anteriormente na seção da PCA. Após apertar o botão "Matriz de dados", a matriz "dados" deve ser selecionada, no botão "Amostras", selecionar "amostras_ab" e, em "Variáveis", selecionar "medidas". Em seguida, os usuários precisam definir alguns parâmetros específicos do SOM, como o tipo da topologia da rede usando o botão "Topologia", número de neurônios em cada uma das dimensões da rede, em "Neurônios dimensão 1" e "Neurônios dimensão 2", a quantidade de épocas de treinamento, em "Épocas de treinamento", e, por fim, marcar a caixa "Auto ajuste", de acordo com a Figura 4b. Para usuários mais experientes, ao desmarcar a caixa "Auto ajuste", outros parâmetros podem ainda ser ajustados. Para mais detalhes destes parâmetros, os leitores podem consultar Haykin.51 Por exemplo, a taxa de aprendizagem da rede, na caixa "Taxa de aprendizagem", é um parâmetro que controla o quanto os pesos dos neurônios são ajustados em cada iteração. Segundo Haykin,28 é recomendável usar uma taxa de aprendizagem inicial com um valor próximo de 0,1; portanto, o GAMMA-GUI tem como default esse valor de taxa de aprendizagem. Agora é hora de realizar a análise dos dados, apertando o botão "Treinamento", que, após finalizada, fornecerá uma estrutura de saída que renomeamos para "som_out_13_13". A fim de poupar o tempo de análise dos dados, neste material de demonstração os usuários têm acesso aos resultados de três opções de saídas de rede, em diferentes configurações, nomeadas como: "som_out_8_8", "som_out_13_13" e "som_out_15_15", que correspondem às topologias de dimensões 8 × 8, 13 × 13 e 15 × 15, respectivamente (Figuras 4c, 4d e 4e). Nestes gráficos, os pontos vermelhos representam os neurônios distribuídos na grade, enquanto as linhas azuis indicam as conexões de vizinhança entre eles. No interior da grade, cada ponto (neurônio) se conecta aos seus vizinhos que os cercam, formando uma estrutura chamada topologia. Neste caso, hexagonal, pois o padrão resultante se assemelha a hexágonos. No entanto, nas bordas e nos cantos da grade, os neurônios possuem menos conexões, pois nem todos os seis vizinhos estão disponíveis. A mesma linha de raciocínio é válida para a topologia retangular. Conforme antecipado, definir os parâmetros do SOM na maioria das vezes, não é uma tarefa trivial e pode exigir uma série de tentativas, mas algumas abordagens facilitam na sua definição, conforme demonstraremos. Durante a escolha da topologia da rede, os usuários devem priorizar uma estrutura de grade hexagonal se os dados tiverem uma distribuição mais isotrópica, ou escolher uma estrutura de grade retangular se os dados tiverem uma distribuição mais linear. Neste exemplo, escolhemos a topologia hexagonal, pois conforme vimos anteriormente, a PCA (técnica linear) não foi suficiente para diferenciar com clareza as três espécies de flores, ver Figura 4a. Outro parâmetro que deve ser ajustado é a quantidade de neurônios na grade, o que altera o tamanho da rede. Esse ajuste deve ser feito testando diferentes quantidades de neurônios. Uma boa opção é iniciar a análise usando uma quantidade de neurônios próximo ao número de amostras. Neste caso, temos 150 amostras, portanto, iniciaremos os testes com uma rede bidimensional 13 × 13. Ao apertar o botão "Topologia", após o treinamento da rede, os usuários podem gerar o gráfico da topologia da rede, que, neste caso, consiste em uma rede com 169 neurônios (Figura 4c). Para verificar se o tamanho da rede é ideal, os usuários podem comparar os comportamentos de distribuição das amostras com redes menores ou maiores (conforme veremos adiante). Neste caso, comparamos os resultados com uma rede 8 × 8, que contém 64 neurônios (Figura 4d), e uma rede 15 × 15, que contém 250 neurônios (Figura 4e). Após a etapa de treinamento da rede, os usuários podem gerar o gráfico de erro de treinamento da rede usando o botão "Erro de treinamento" (Figura 4f). Além das opções gráficas, os usuários podem acessar uma série de outros resultados da análise nas estruturas de saída dos dados, neste caso nomeadas como "som_out_8_8", "som_out_13_13" e "som_out_15_15", disponíveis no material demonstrativo deste tutorial. O gráfico de erro de treinamento auxilia os usuários na definição do número de épocas de treinamento, ou seja, o número de vezes que o conjunto de dados de treinamento é apresentado à rede. Ao utilizar um número elevado de épocas, a rede pode sofrer overfitting, memorizando os dados de treinamento em vez de aprender novos padrões, diminuindo a capacidade de generalização. Se o número de épocas for baixo, pode ocorrer o underfitting.28,53 Na rede 13 × 13 testada, o erro de quantização no gráfico decresce com o aumento do número de épocas (Figura 4f), e, após 4000 épocas, o erro de quantização atinge um estado estacionário. Esse platô no gráfico indica que os neurônios no mapa estão próximos de representar corretamente os padrões de entrada observados. Portanto, as 5000 épocas definidas na caixa "Épocas de treinamento" foram suficientes para esse conjunto de dados. Caso um platô não seja atingido, seria apropriado considerar o treinamento de uma nova rede com um número maior de épocas. Por outro lado, se um platô for alcançado com menos épocas, os usuários podem optar por utilizar menos épocas, resultando em uma redução considerável no tempo de treinamento da rede. O mapa topológico é uma das principais representações gráficas do SOM, permitindo visualizar a distribuição das amostras de acordo com o neurônio vencedor. No botão "Mapa topológico" do GAMMA-GUI, existem diversas opções de gráficos para os dados, como o uso da caixa de identificação das amostras por "Numeração" ou "Grupos", e a caixa de seleção das amostras a serem plotadas, que podem ser "Todas as amostras" ou grupo específico das amostras que se deseja plotar, neste caso "A", "B" ou "C". Além disso, os usuários podem ainda incluir a topologia da rede no mapa topológico, marcando a caixa "Incluir topologia". Nas Figuras 3Sa-3Sc (Material Suplementar), temos os mapas topológicos para as três configurações testadas. Nestes gráficos, cada amostra do conjunto de dados está associada a um respectivo neurônio "vencedor", ou seja, aquele neurônio que melhor o representa na rede. Por ser uma técnica aglomerativa não supervisionada, o SOM organiza os dados de entrada como clusters, que podem ser formados por um ou mais neurônios. A definição de clusters é caracterizada pela presença de neurônios vazios entre os grupos. Clusters próximos compartilham semelhanças; ou seja, quanto maior a distância euclidiana, maior a diferença entre os clusters.54 Interpretando os resultados do SOM para esse conjunto de dados, obtidos com diferentes tamanhos de rede, nota-se que as amostras de Iris tendem a formar clusters. Comparando o perfil de distribuição das amostras entre as redes de 13 × 13 e 8 × 8 nas Figuras 3Sa e 3Sb, percebe-se que a redução no tamanho da rede resulta em uma significativa sobreposição das amostras A, B e C nos mesmos neurônios. Isso sugere fortemente que um aumento no tamanho da rede é indicado para melhorar a representação dos dados, evitando a perda de informações devido à superposição excessiva de amostras diferentes no mesmo neurônio. Ao comparar a distribuição entre as redes de 13 × 13 e 15 × 15 das Figuras 3Sa e 3Sc, observa-se que o aumento no tamanho da rede resultou apenas em uma maior dispersão das amostras no mapa, sem melhoria no agrupamento das classes de Iris. Essas comparações sugerem que uma rede de tamanho 13 × 13 é apropriada, indicando que o aumento da rede não trouxe benefícios adicionais. Conforme observado na Figura 3Sa, há uma certa diferenciação entre as três espécies de flores Iris. No entanto, assim como ocorreu na análise PCA, ainda existe alguma sobreposição entre as amostras de Iris versicolor (A) e Iris virginica (B). Nota-se que, à direita do mapa, identificamos claramente a formação de um cluster representado pelas flores Iris setosa (C), no centro encontra-se o cluster majoritariamente composto pelas flores Iris versicolor (A), e à esquerda do mapa o cluster formado pelas flores Iris virginica (B). Esse resultado demonstra que os desempenhos obtidos com o SOM podem ser comparáveis aos da PCA. No entanto, as abordagens de análise de dados aplicadas são totalmente distintas, sendo a PCA um modelo quimiométrico e o SOM um modelo de aprendizagem. Outra saída gráfica do SOM é o mapa de hits. Ao clicar no botão "SOM hits", o usuário pode visualizar um gráfico que contabiliza quantas amostras foram atribuídas a cada "neurônio vencedor" (Figura 3Sd). Já o mapa de pesos é uma representação visual indicada por escalas de cores no gráfico, que associa o mapa topológico à segmentação das amostras, baseada nos pesos dos neurônios em relação às variáveis de entrada, de forma semelhante aos pesos na PCA. Neste gráfico, cada neurônio na rede possui um vetor de pesos que define sua resposta a determinados padrões nos dados de entrada. Assim, a interpretação de um mapa de pesos envolve analisar como esses vetores estão distribuídos no espaço do mapa e representados pela escala de cores.54 No GAMMA-GUI, os usuários têm a capacidade de escolher o tipo de mapa de pesos que desejam criar através da opção "Tipo de gráfico". Ao escolher "Contorno", serão gerados gráficos em duas dimensões, enquanto a seleção de "Superfície" resultará em gráficos em três dimensões. Um mapa de peso é gerado para cada variável. Portanto, basta que o usuário ajuste em "Variável selecionada" qual variável deseja analisar e, em seguida, apertar o botão "Plotar". Neste exemplo, as variáveis são as quatro características taxonômicas medidas: comprimento da sépala, largura da sépala, comprimento da pétala e largura da pétala. Assim, quatro mapas de pesos em duas dimensões foram gerados (Figuras 5a-5d). Os usuários também podem criar os mapas de pesos em três dimensões (não mostrado).
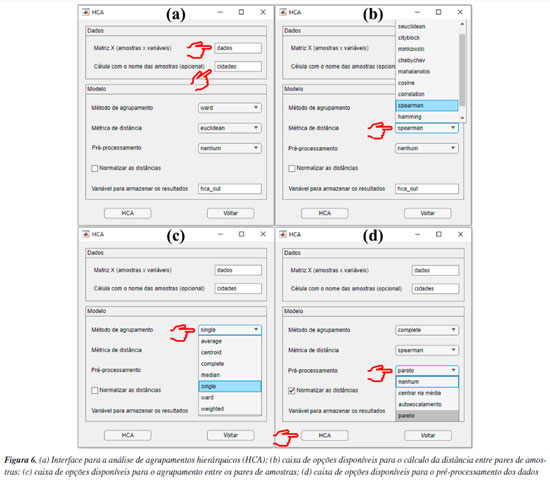
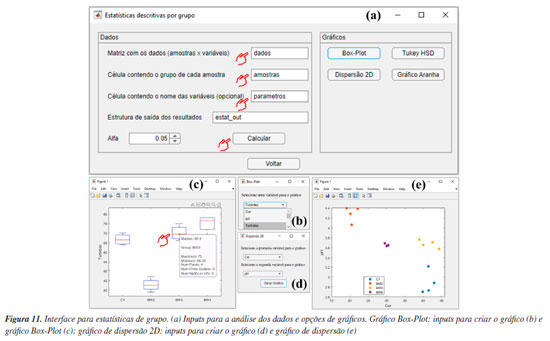
Analisando os mapas de pesos das Figuras 5a-5d, observa-se que as amostras de Iris setosa (C) na maioria dos casos exibem pesos menores em comparação com as amostras de Iris versicolor (A) e Iris virginica (B), enquanto as amostras de Iris virginica (B), por sua vez, demonstram pesos superiores às amostras de Iris versicolor (A). Essa distribuição heterogênea dos pesos no mapa para cada classe de amostras de flores significa que as quatro variáveis podem influenciar na formação dos clusters. No entanto, é notável que, entre as quatro variáveis analisadas, a largura e o comprimento da pétala foram as variáveis mais importantes. Isso é possível ao observar a escala de cores, para diferenciar claramente as três espécies de flores Iris. Tal comportamento não é observado para a largura da sépala (Figura 5b), uma vez que, segundo a escala de cores, não é possível evidenciar com clareza a diferenciação entre as espécies de flores. Uma abordagem alternativa consiste em realizar o treinamento de uma nova rede utilizando as mesmas configurações, porém removendo a variável "largura da sépala" do conjunto de dados para tentar melhorar a diferenciação entre as amostras. Tal abordagem também é aplicada na PCA, quando uma variável prejudica a diferenciação das amostras. De acordo com a Figura 4S (Material Suplementar), observa-se que, ao utilizar o conjunto de dados "som_out_13_13_sem_var2", isto é, a coluna da matriz que corresponde à largura da sépala, o perfil de diferenciação entre as três espécies de Iris teve uma ligeira melhora comparada à análise anterior. Para concluir esta seção, gostaríamos de ressaltar que a inclusão do SOM neste tutorial tem como principal objetivo apresentar uma alternativa entre várias possíveis para a análise exploratória de dados, podendo complementar a PCA. Nosso foco é mostrar como executar e interpretar os resultados do SOM, uma abordagem ainda pouco usual na quimiometria. Isso não significa que o SOM seja melhor ou pior do que a PCA. Neste exemplo, os resultados foram semelhantes, mas o SOM pode ser uma opção interessante para testes adicionais, especialmente em casos em que a PCA não seja suficientemente informativa. HCA Utilizamos, neste exemplo um conjunto de dados composto por 20 variedades de soja (Glycine max (L.) Merrill), desenvolvidas pela EMBRAPA-Soja e recomendadas para o plantio na região Centro-Sul do Brasil. As 20 amostras de soja foram simultaneamente cultivadas em Londrina e Ponta Grossa, totalizando 40 amostras que foram quantificadas quanto à composição inorgânica (K, P, Ca, Mg, S, Zn, Mn, Fe, Cu e B) por ICP-OES (do inglês, inductively coupled plasma optical emission spectroscopy). Mais detalhes podem ser obtidos em Cremasco et al.53 Durante o experimento, as plantas foram submetidas às mesmas condições de fertilização e tratamento de irrigação, embora as duas cidades tenham características distintas de clima, terreno e temperaturas. Utilizando a diversidade do conjunto de dados, verificaremos a capacidade de agrupamentos das amostras usando HCA com base no perfil mineral, considerando a localização geográfica do cultivo. Esse conjunto de dados consiste em 40 amostras, igualmente distribuídas entre Londrina e Ponta Grossa, com 10 elementos determinados, resultando em uma matriz X de dimensões 40 × 10, disponível em "dados_soja" e YouTube.55 Ao carregar o material de demonstração, os usuários têm acesso à matriz "dados", que consiste nos valores obtidos para os 10 elementos quantificados em cada amostra. Além disso, há um vetor que contém as cidades de plantio de cada amostra, denominado "cidades", e um vetor com os símbolos dos elementos químicos determinados, chamado "var". A próxima etapa envolve a definição dos inputs da HCA na interface "HCA" disponível na janela "Análise Exploratória" do GAMMA-GUI. Nesta nova interface, os usuários devem inserir o nome da matriz "dados" na caixa "Matriz X (amostras × variáveis)" e o vetor contendo os nomes das amostras, denominado "cidades", na caixa "Célula com o nome das amostras (opcional)", conforme mostrado na Figura 6a.
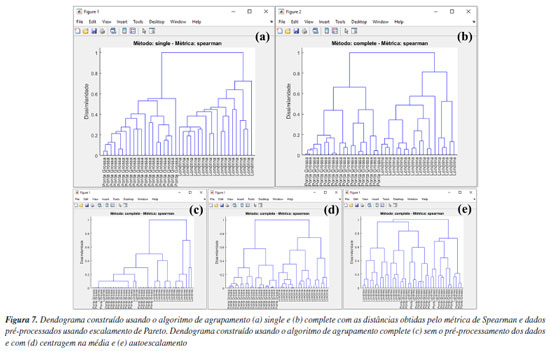
Por ser bem estabelecida há tempos, existe uma série de algoritmos disponíveis para a HCA.3 Portanto, uma forma de estimar a semelhança entre amostras é através do cálculo da distância entre elas. Usando a caixa "Métrica de distância", os usuários têm à disposição uma série de alternativas para estimar as distâncias entre pares de amostras (Figura 6b). Não existe uma regra geral para a escolha da distância que deve ser utilizada na HCA, e cada opção deve ser avaliada individualmente. Portanto, cabe aos usuários avaliarem separadamente as características de seus dados e tomar decisões sobre a métrica de distância que melhor se adequa aos objetivos da análise. Entre todas as possibilidades de métricas, a distância "euclidiana", "cityblock" (Manhattan) e "mahalanobis" são as mais populares entre os químicos. Para mais detalhes, consultar Ferreira.3 Entretanto, neste exemplo, após testar diferentes métricas, chegamos à conclusão de que a opção "spearman" produziu resultados mais adequados. Apesar de ser pouco comum, o coeficiente de correlação de Spearman (ρ) pode ser utilizado como métrica de distância na HCA.1 O coeficiente de correlação de Spearman (ρ) pode ser transformado em uma medida de dissimilaridade (distância) definida como: DSpearman(x, y) = 1 - ρ(x, y), onde DSpearman é a medida de dissimilaridade usada na HCA. Após definir a métrica para a estimativa das distâncias entre os pares de amostras, é hora de definir o método de agrupamento das amostras usando uma das opções na caixa "Método de agrupamento". No GAMMA-GUI, há uma série de alternativas de agrupamento disponíveis (Figura 6c), sendo os mais frequentes para os químicos o algoritmo do vizinho mais próximo "single", mais distante "complete", pela média "median", centroide "centroid" e de Ward "ward".3 A escolha do algoritmo de agrupamento depende da estrutura do conjunto de dados. Se os grupos estão bem discriminados, qualquer opção pode ser utilizada. Entretanto, se há uma sobreposição entre ou grupos ou alta proximidade entre eles, é preferível que usuários comparem os resultados entre os algoritmos do vizinho mais próximo (single) e mais distante (complete). Se os resultados forem iguais, isso sugere que as amostras estão naturalmente organizadas em grupos distintos.3 Neste caso, a comparação dos resultados entre os algoritmo single e complete, expressos nas Figuras 7a e 7b, revela que as amostras estão naturalmente organizadas em dois conjuntos distintos, uma vez que as amostras de Londrina e Ponta Grossa podem ser facilmente distinguíveis em ambos os casos, de acordo com um índice de dissimilaridade próximo a 0,8 (salto considerável na distância em relação à etapa anterior). Caso esse comportamento não fosse evidenciado, outra opção de análise de dados, como a PCA deve ser considerada.3 Nos dendrogramas da Figura 7, os índices de dissimilaridade (eixo das ordenadas) estão expressos em distâncias normalizadas. Para isso, basta os usuários marcarem a caixa "Normalizar as distâncias".
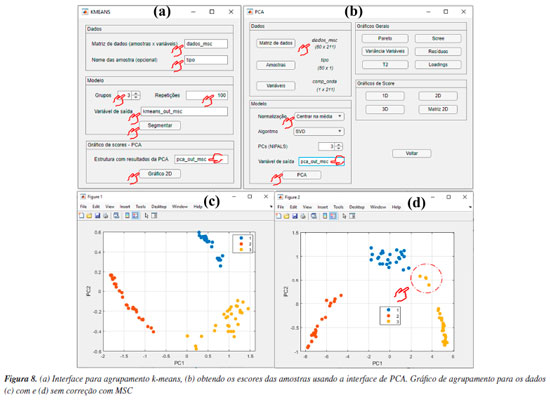
Por ser versátil, com várias possibilidades de combinações entre estimativas de métricas de distâncias e algoritmos de agrupamento, uma maneira eficaz de avaliar os resultados da HCA é através dos dendrogramas. Na Figura 7, temos os dendrogramas, uma representação gráfica na forma de um diagrama de árvore que exibe os agrupamentos (clustering) formados em cada passo e em seus níveis de similaridade. Cada nó no dendrograma representa um cluster ou um ponto de dados individual, e os ramos conectam os nós de acordo com a proximidade dos elementos, sendo que o tamanho dos ramos fornece o grau de dissimilaridade entre os grupos.54 Outro fator que deve ser considerado na análise dos dados é a aplicação do pré-processamento, conforme abordado na seção PCA. Na opção "Pré-processamento", os usuários podem testar diferentes possibilidades de pré-processamentos (Figura 6d). Neste caso, a comparação dos resultados entre os pré-processamentos de dados pode ser visualizada nas Figuras 7b-7e. Fica evidente nestes gráficos a importância da escolha do pré-processamento adequado, de modo que os resultados de agrupamento foram equivalentes usando Pareto (Figura 7b) ou centragem na média (Figura 7d), enquanto a ausência de pré-processamento (Figura 7c) ou a aplicação de autoescalamento (Figura 7e) pioraram os desempenhos, visto que amostras de Londrina foram agrupadas no grupo de Ponta Grossa e vice-versa. k-Means Nesta demonstração, vamos agrupar amostras de leites comerciais de acordo com o teor de gordura, utilizando dados espectrais adquiridos em um espectrômetro NIR portátil. Utilizaremos uma fração do conjunto de dados relatado no trabalho de Galvan et al.,56 que consiste em 80 amostras de leite, das quais 28 são amostras de leite integral (LI), 23 de leite desnatado (LD) e 29 de leite semidesnatado (LSD). A matriz X é composta por I linhas, que compreendem às amostras de leites, e J colunas, que correspondem aos comprimentos de onda em nanômetros, gerando uma matriz de dimensões 80 × 228, disponível no material de demonstração "dados_leite" e no YouTube.57 Desta vez, iniciaremos nossa demonstração utilizando a interface "Visualização e pré-tratamentos" (Figura 1Sa) para plotar o gráfico dos espectros e realizar o pré-tratamento dos dados. Nesta interface, aperte o botão "Plotar dados" e siga as instruções de preenchimento mostrados na Figura 5Sa (Material Suplementar). Durante a plotagem dos dados, os usuários têm a flexibilidade de criar suas próprias opções de rotulagem dos dados, entre outras opções, como excluir amostras do gráfico ou plotar classes específicas. Na Figura 5Sb, temos o gráfico dos espectros brutos das amostras. A análise visual dos espectros fornece informações importantes sobre como prosseguir no pré-processamento dos dados. Neste caso, é notável um deslocamento na linha de base nas ordenadas do espectro, possivelmente causado por efeitos de espalhamento aditivo e multiplicativo na absorbância, fenômenos característicos em espectros NIR. Observa-se ainda que, a partir de 1650 nm, ocorre um comportamento atípico no espectro, com aumento do ruído que se sobrepõe aos sinais dos espectros, e um ruído discreto entre 1400 e 1500 nm. Esses ruídos, resultantes da menor sensibilidade do detector ou da baixa intensidade da radiação em comprimentos de onda mais elevados, podem comprometer a análise dos dados. Em espectroscopia NIR, os pré-processamentos mais frequentemente aplicados incluem o uso de derivadas para a correção de efeitos aditivos, além de algoritmos como MSC ou SNV para corrigir efeitos multiplicativos e aditivos na absorbância. Além disso, algoritmos de alisamento, como a média móvel ou o filtro de Savitzky-Golay, são comumente empregados para reduzir o ruído nos espectros. É recomendável que os usuários testem diferentes opções de pré-processamento disponíveis no aplicativo. Para mais detalhes sobre os pré-processamentos, os leitores podem consultar Ferreira.3 Neste exemplo, após alguns testes, verificamos que cortar os espectros entre 900 e 1650 nm e aplicar o MSC foi suficiente para o agrupamento eficiente das amostras. Embora fosse possível aplicar também a primeira derivada com alisamento de Savitzky-Golay para corrigir efeitos de linha de base e ruído, os resultados obtidos foram similares, e por isso optamos por não incluir essa etapa extra. Para cortar os espectros, os usuários devem clicar no botão "Selecionar variáveis" e, em seguida, definir a matriz de dados (correspondente aos espectros brutos), o vetor de intensidades (relacionado aos comprimentos de onda) e, por fim, especificar a faixa desejada no campo apropriado, conforme indicado no aplicativo. Após cortar os espectros, a estrutura "sel_out" aparecerá no workspace do Matlab. Acessando essa estrutura, o usuário encontrará a matriz X com os espectros cortados, chamada "dados", e um vetor "faixa", que representa os comprimentos de onda dos espectros entre 900 e 1650 nm. Esses dados podem ser extraídos da estrutura (opcional). Para isso, basta clicar na matriz "dados", acessar a aba superior "VARIABLE" do software e, em seguida, clicar no botão "New from Selection" (ícone "+" amarelo no canto superior esquerdo), repetindo o mesmo procedimento para o vetor "faixa". Optamos por renomear a matriz "dados" para "dados_brutos" e o vetor "faixa" para "comp_onda", substituindo-os pelos dados cortados. Caso o usuário prefira não substituir os originais, basta atribuir novos nomes às variáveis. Ou, na linha de comando da "Command Window" (>>), o usuário pode escrever dados_brutos = sel_out.dados e comp_onda = sel_out.faixa. Em seguida, aplicaremos o algoritmo MSC na matriz de dados X cotada, ou seja, contendo a faixa espectral entre 900 e 1650 nm. Para isso, basta apertar o botão "Correção de sinal" e seguir as instruções de preenchimento da Figura 5Sc. Comparando os espectros das Figuras 5Sb e 5Sd, observa-se a correção do deslocamento na linha de base e a exclusão da região após 1650 nm. Após aplicar a correção com MSC, a estrutura "xcor_out" aparecerá no workspace do Matlab. Acessando essa estrutura, o usuário encontrará a matriz X com os espectros corrigidos, chamada "dados", que pode ser extraída da estrutura (opcional). Para isso, basta clicar na matriz "dados" e seguir o procedimento descrito anteriormente, renomeando-a para "dados_msc". Alternativamente, o usuário pode usar a linha de comando da "Command Window" digitando: dados_msc = xcor_out.dados. A próxima etapa envolve o uso do k-means na interface "Análise Exploratória". Nesta interface, aperte o botão "KMEANS" e inicie definindo os inputs nas caixas disponíveis da nova janela que se abrirá, inserindo o nome da matriz de dados "dados_msc" na caixa "Matriz de dados (amostras × variáveis)" e o nome das amostras "tipo" na caixa "Nomes das amostras (opcional)", conforme ilustrado na Figura 8a. O número de grupos deve ser ajustado para três usando o botão "Grupos", pois, neste caso, temos três tipos de leite (integral, semidesnatado e desnatado). Essa etapa não torna o k-means um algoritmo de aprendizado supervisionado, pois não depende de dados de entrada rotulados para treinamento.1 Caso não se saiba a quantidade de grupos, é possível fazer o modelo com diferentes quantidades de grupos e comparar qual produz uma segmentação mais adequada. Por fim, o número de repetições que os dados serão avaliados deve ser definido na caixa "Repetições", sendo cem repetições o default do aplicativo. O k-means é um algoritmo que inicia a localização do centro dos grupos aleatoriamente, portanto, a cada vez que é executado, o resultado pode ser ligeiramente diferente. Assim, como resultado, cada amostra será atribuída à classe na qual foi classificada na maioria das vezes, considerando todas as repetições realizadas.
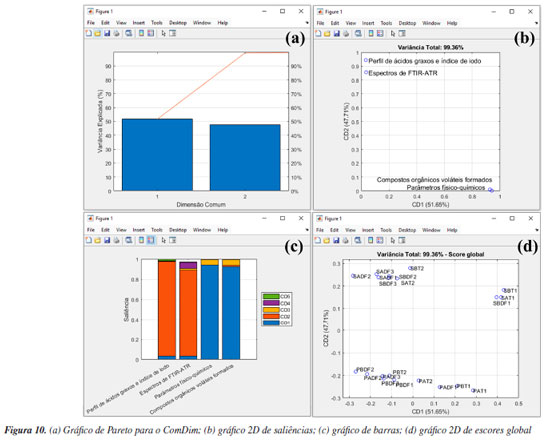
Antes da segmentação dos dados na caixa "Variável de saída", optamos por redefinir o nome da estrutura de saída dos resultados para "kmeans_out_msc", pois, adiante, iremos comparar os resultados com e sem a correção MSC. Essa comparação tem apenas o objetivo demonstrativo, para destacar a importância da etapa de pré-processamento antes da análise dos dados. É importante deixar claro aos leitores que não é adequado realizar a análise dos dados sem a execução prévia das etapas de pré-tratamento. Após essas etapas, apertar o botão "Segmentar" e, em poucos segundos, a análise será finalizada, gerando a estrutura "kmeans_out_msc" no workspace do Matlab. Na estrutura recém-criada, os usuários têm acesso aos resultados de agrupamento das amostras em "grupos", entre outros resultados da análise. Na estrutura "grupos", há três subestruturas que correspondem aos três grupos previamente estabelecidos. Ao acessar cada uma das subestruturas, os usuários podem verificar quais tipos de amostras foram agrupadas neste respectivo grupo. Neste caso, é possível observar que cada grupo contém somente amostras LSD, LD e LI. Uma opção gráfica dos resultados do k-means é a "projeção" dos agrupamentos nos escores das amostras obtidos com PCA. Para isso, é necessário realizar uma PCA para o mesmo conjunto de dados, conforme ilustrado na Figura 8b. Após a realização da PCA, retorne para a interface do k-means e, na caixa "Estrutura com resultados da PCA", o usuário precisa digitar o nome da estrutura de saída da PCA, neste caso "pca_out_msc", e então apertar o botão "Gráfico 2D". Na opção de gráfico 2D, o usuário pode escolher quais PCs deseja plotar, sendo que, neste caso, escolhemos a PC1 vs. PC2, ver Figura 8c. Para fins comparativos, realizamos o mesmo procedimento descrito anteriormente, mas desta vez, utilizando o conjunto de dados sem correção com MSC "dados_brutos", e obtivemos a Figura 8d. Ao projetar os resultados do agrupamento k-means nos escores da PC1 vs. PC2 gerados pela PCA, é notável a importância do pré-processamento aplicado, neste caso, a correção por MSC (Figuras 8c e 8d). Com a correção MSC, os leites semidesnatado (azul), desnatado (vermelho) e integral (amarelo) formam três agrupamentos distintos e bem definidos. Em contraste, ao utilizar os dados sem a correção MSC (Figura 8d), quatro amostras de leite semidesnatado (marcadas em amarelo no gráfico) foram erroneamente agrupadas no cluster das amostras de leite integral (azul). ComDim Nesta demonstração, exploraremos a estabilidade oxidativa da oleína de palma refinada e do óleo de soja parcialmente hidrogenado, submetidos ao processo de fritura industrial de produtos cárneos de frango usando a análise multibloco/multitabela.58 O conjunto de dados fornecido, denominado "dados_oleos", abrange quatro matrizes distintas, conforme vídeo no YouTube.59 A primeira matriz, compreende o perfil de ácidos graxos e índice de iodo, determinados por GC-FID (do inglês, gas chromatography-flame ionization detector), em 20 amostras de óleos, gerando uma matriz de dimensões 20 × 18, denominada "FAP". A segunda matriz, é composta pelos dados de fingerprint obtidos por FTIR-ATR (do inglês, Fourier transform infrared spectroscopy-attenuated total reflectance), gerando uma matriz de dimensões 20 × 2479, denominada "FTIR". A terceira matriz engloba a determinação de 6 parâmetros físico-químicos, resultando em uma matriz de dimensões 20 × 6, denominada "PC". Por fim, a quarta matriz incorpora dados da determinação de compostos orgânicos voláteis formados, analisados por SPME (do inglês, solid phase microextraction) e GC-FID, resultando em uma matriz 20 × 8, denominada "VOC". No vetor "amostras", os usuários têm acesso à identificação das amostras. As amostras iniciadas com a letra "P" representam a oleína de palma, enquanto as iniciadas em "S" correspondem ao óleo de soja. A segunda letra identifica os dois produtos cárneos de frango, sendo "A" e "B" submetidos à fritura. Além disso, as letras "T1" e "T2" representam o tanque de armazenamento antes e após a fritura, respectivamente. Já as amostras identificadas como "DF1", "DF2" e "DF3" referem-se ao tanque da fritadeira após 1, 2 e 3 h do processo de fritura. Mais detalhes podem ser encontrados em Silva et al.58 O ComDim é uma análise multibloco exploratória de dados, desenvolvido para extrair informações comuns de dados gerados a partir de diferentes fontes, ou seja, conjuntos de dados diferentes adquiridos para as mesmas amostras. Nesse sentido, o emprego do ComDim fundamenta-se na condição de que as matrizes de dados tenham apenas o mesmo número de linhas, não sendo obrigatório que tenham o mesmo número de colunas. Além disso, é fundamental observar que as amostras devem estar dispostas na mesma ordem em todas as matrizes de dados avaliadas.33,34,38 A principal vantagem do ComDim, comparada à PCA, reside na sua capacidade de realizar a extração de características relevantes de cada fonte de dados simultaneamente em uma única etapa, graças à sua natureza multibloco. Isso elimina a necessidade de conduzir diversas análises PCA separadas, simplificando e melhorando consideravelmente a interpretação dos dados. Além disso, a análise das saliências permite avaliar se os dados de diferentes fontes apresentam informações comuns ou complementares, e qual o peso de cada tabela nas dimensões comuns geradas. Na janela "Análise Exploratória" do GAMMA-GUI, os usuários precisam apertar o botão "ComDim", e uma janela semelhante a Figura 9a se abrirá. Uma etapa fundamental que antecede a análise dos dados consiste na geração da estrutura que contém cada conjunto de dados, que tem como default a nomenclatura "comdim_in". Iniciamos a construção da estrutura definindo alguns inputs fundamentais, como a definição opcional do vetor que contém o nome das amostras, digitando "amostras" na caixa "Vetor das amostras (opcional)". Na etapa seguinte, o usuário precisa ajustar, usando o botão "Quantidade de tabelas", o número de tabelas avaliadas, neste caso, são quatro tabelas. Então, deve apertar o botão "Dados workspace". Após isso, uma nova janela semelhante à Figura 9b se abrirá. Neste exemplo, utilizamos dados que já estavam no workspace previamente carregados. No entanto, se o conjunto de dados utilizado estiver em uma planilha do Excel, os usuários podem ainda usar o botão "Ler planilha" para gerar a estrutura de dados.
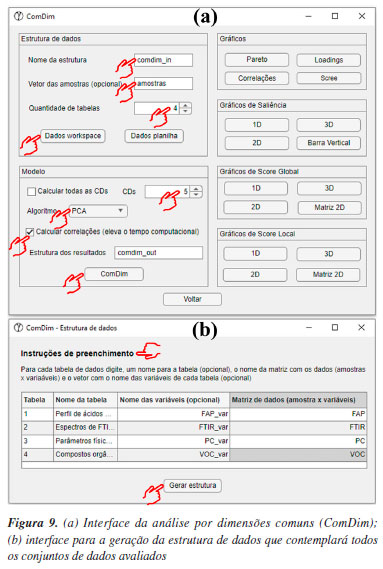
Para o preenchimento da interface "ComDim - Estrutura de dados", os usuários devem seguir as instruções de preenchimento na própria janela. Nesta tabela, é opcional o preenchimento da caixa "Nome da tabela", na qual os usuários podem nomear cada conjunto de dados que será inserido na estrutura "comdim_in", criando suas próprias nomenclaturas. É fundamental salientar que cada conjunto de dados deve obedecer à mesma ordem em todas as demais caixas preenchidas. Neste exemplo, adotamos a seguinte nomenclatura e ordem: "Perfil de ácidos graxos e índice de iodo", "Espectros de FTIR-ATR", "Parâmetros físico-químicos" e, por fim, "Compostos orgânicos voláteis formados". Outra opção de preenchimento opcional é a caixa "Nome das variáveis (opcional)". Nesta caixa, os usuários podem identificar as variáveis, ou seja, fornecer os nomes das colunas de cada conjunto de dados. Neste caso, temos três vetores que incluem os nomes das colunas e um vetor com os valores correspondentes aos números de onda dos espectros de FTIR. Seguindo a ordem previamente estabelecida, iniciamos definindo o vetor que contém os nomes dos perfis de ácidos graxos determinados, digitando "FAP_var". Posteriormente, definimos o vetor com os comprimentos de onda, digitando "FTIR_var". Em seguida, especificamos o vetor que contém os nomes dos parâmetros físico-químicos determinados, digitando "PC_var" e, finalmente, o vetor com os nomes dos compostos orgânicos voláteis formados, digitando "VOC_var". Na etapa final da geração da estrutura, os usuários devem definir as matrizes correspondentes a cada conjunto de dados na caixa "Matriz de dados (amostra × variáveis)". Nessa caixa, é necessário inserir os nomes "FAP", "FTIR", "PC" e "VOC", conforme exemplificado na Figura 9b. Após a definição dos inputs requeridos, é hora de gerar a estrutura "comdim_in" apertando o botão "Gerar estrutura", que logo aparecerá no workspace do Matlab. Acessando a estrutura "comdim_in", os usuários têm disponível informações acerca das amostras, vetores das variáveis e matrizes de dados. Uma vez gerada a estrutura de dados, não há mais necessidade de realizar novamente este procedimento, caso os conjuntos de dados permaneçam inalterados. Agora é hora da análise dos dados, para isso, basta eleger o critério de escolha do número de dimensões comuns (CDs), que pode ser "Calcular todas as CDs" ou definir a quantidade de CDs na caixa "CDs". Neste exemplo, definimos o número de CDs igual a cinco. Não é recomendável o cálculo de todas as CDs para matrizes muito grandes, pois o cálculo computacional pode ser demorado e dificilmente será necessária a análise de todas as CDs. Por fim, é preciso ainda escolher o algoritmo para a decomposição dos dados usando o botão "Algoritmo", que conta com três opções disponíveis: uma por "PCA", uma por "CCA" e outra por "ICA". Para mais detalhes sobre cada uma destas opções, os leitores podem consultar Bouveresse e Rutledge.35 Neste exemplo, utilizaremos a opção "PCA" e ainda marcaremos a caixa "Calcular correlações" para obter os valores de correlações entre as CDs. Por fim, devemos apertar o botão "ComDim". Durante a escolha do número de CDs e obtenção das correlações, é recomendável que os usuários considerem usar a opção que possibilita definir uma quantidade de CDs, e ainda desmarcar a opção para os cálculos de correlações, caso os conjuntos de dados sejam grandes. Caso contrário, dependendo da capacidade de processamento do computador o tempo de análise dos dados pode ser considerável. Após finalizar a análise dos dados uma estrutura chamada "comdim_out" (nome de default) será gerada no workspace do Matlab. Nesta estrutura, os usuários têm acesso a uma série de resultados da análise, como o algoritmo escolhido em "metodo", número de CDs em "CDs", os dados analisados em "data", a matriz de correlação em "correlacoes" e, por fim, a estrutura "model". Na estrutura "model", os usuários têm acesso a diversos resultados, tais como a matriz de Frobenius em "Xn_mat", a variância explicada em "variancia", as saliências individuas em "saliencias", e a soma das saliências em cada CD e tabela em "Soma_sal_dim" e "Soma_sal_tab", respectivamente. A matriz "ValSing" contém os valores singulares (autovalores), na matriz "T", os valores de escores globais, em "P", os pesos globais normalizados e, em "L", os pesos globais não normalizados, enquanto as estruturas "Tlocal", "Plocal" e "Llocal" contém os escores e pesos de cada conjunto de dados individual. É fundamental esclarecer que, no ComDim, cada CD extraída possui um conjunto de saliências, escores e pesos. A saliência é o peso/contribuição atribuído a cada bloco para a construção de uma CD específica, que também pode ser interpretada como a variância do bloco representada naquela CD. Já os escores são as projeções das amostras no espaço comum da CD, e os loadings são os pesos das variáveis contidas em cada bloco, tendo uma interpretação análoga à da PCA.34 Na interface do ComDim, os usuários têm acesso a diversos recursos gráficos. Para iniciar a análise dos resultados, pressionaremos o botão "Pareto" para gerar o gráfico de Pareto (Figura 10a). Semelhante ao gráfico de Pareto da PCA, no ComDim, esse gráfico, juntamente com o gráfico de Scree, oferecem aos usuários a capacidade de determinar o número ideal de CDs a serem consideradas no estudo. Neste exemplo, inicialmente optamos por avaliar as cinco primeiras CDs. No entanto, ao analisar o gráfico, observamos que as duas primeiras CDs foram suficientes para representar 99,36% da variância nos quatro blocos de dados, com 51,65% da variância representada na CD1 e 47,71% na CD2.
Após constatar o número ideal de CDs, os usuários podem prosseguir com a análise, gerando os gráficos de saliências. No GAMMA-GUI, existe a possibilidade de gerar o gráfico de saliência em uma, duas ou três dimensões, ou ainda gerar o gráfico de barra vertical. Neste exemplo, vamos gerar o gráfico de saliência em duas dimensões, considerando que duas CDs são suficientes para explicar mais de 99% da variabilidade dos conjuntos de dados. Para isso, na caixa "Gráficos de Saliência" ao apertar o botão "2D", os usuários precisam definir qual CD estará no eixo x e y do gráfico. Neste caso, optamos por plotar as saliências da CD1 no eixo x e da CD2 no eixo y, e então apertar o botão "Plotar" (Figura 10b). É importante ressaltar que os usuários têm a flexibilidade de criar gráficos conforme suas necessidades. Por exemplo, se desejarmos plotar as saliências das CDs 3 e 4, bastaria indicar o número 3 e 4 nos eixos. Se o objetivo é criar um gráfico 3D, basta inserir os números das CDs que se deseja representar nos eixos x, y e z. Outra opção é criar um gráfico que relaciona o valor de saliência para cada conjunto de dados em cada CD específica, apertando o botão "Barra Vertical" (Figura 10c). De acordo com os gráficos das Figuras 10b e 10c, fica evidente que os maiores valores de saliências na CD1 são dos blocos dos parâmetros físico-químicos (saliência de 0,941) e composto orgânicos voláteis (saliência de 0,927). Enquanto na CD2 as maiores saliências são dos blocos de perfil de ácidos graxos/índice de iodo (saliência de 0,942) e FTIR (saliência de 0,855). Os valores de saliências podem ainda serem encontrados na matriz "saliencias" dentro da estrutura "comdim_out.model". Cabe ainda salientar que as saliências também podem ser interpretadas como a variância do bloco representada nesta CD. Os valores de saliências desempenham um papel crucial no ComDim, e, com base nesses valores, podemos concluir neste estudo que os dados provenientes da análise físico-química e dos compostos voláteis compartilham informações comuns para diferenciar amostras na CD1. Por outro lado, dados do perfil de ácidos graxos e FTIR compartilham informações comuns para diferenciar amostras na CD2. Entretanto, os conjuntos de dados da CD1 apresentam informações complementares à CD2, ou seja, as informações que permitem diferenciar as amostras não são as mesmas. Outro recurso do GAMMA-GUI é o gráfico de escores global (refere-se aos escores dos objetos nas dimensões comuns identificadas através da análise ComDim) e local (refere-se aos escores dos objetos nas dimensões específicas de cada conjunto de dados individual). Os gráficos de escores podem ser gerados em uma, duas e três dimensões, ou ainda usando a opção de matriz 2D. Na caixa "Gráficos de Score Global", os usuários precisam definir qual(is) CD(s) estarão nos eixos do gráfico. Novamente, optamos por plotar as projeções das amostras em 2D. Para isso, basta apertar o botão "2D" e escolher a CD1 no eixo x e a CD2 no eixo y. Na caixa de identificação das amostras, escolha "Nome", e então aperte o botão "Plotar". No gráfico de escores global (Figura 10d), nota-se que a CD2 possibilitou a diferenciação das amostras de acordo com o tipo de gordura utilizada no processo de fritura, com as amostras de óleo de soja (S) localizadas no quadrante positivo da CD2 e as amostras de palma (P) no quadrante negativo. Embora a CD2 não possibilite evidenciar a diferenciação das amostras com base no tipo de produto frito (A ou B) ou nos pontos de amostragem (T1, T2, DF1, DF2 e DF3). Baseado nos valores de saliências da CD2 discutidos anteriormente, os conjuntos de dados do perfil de ácidos graxos e de FTIR foram predominantes nesta CD. Isso significa que essas metodologias analíticas são responsáveis por separar as amostras de acordo com o tipo de gordura utilizada. Porém, não foram capazes de diferenciar as amostras que sofreram estresse térmico pelo processo de fritura. Já, na CD1 é possível observar uma certa separação das amostras de acordo com o ponto de amostragem. Observa-se que maioria das amostras que não foram utilizadas no processo (T1) ou que foram utilizadas por menor período (DF1) estão localizadas no quadrante positivo da CD1, com apenas uma amostra T2 neste quadrante. Enquanto as demais amostras utilizadas no processo de fritura apresentam escores negativos na CD1. Neste caso, a separação das amostras de acordo com o tipo de produto ou tipo de óleo usado no processo de fritura não é evidente nesta CD1. Porém, os dados das análises físico-químicas e dos compostos orgânicos voláteis forneceram informações comuns para a diferenciação das amostras de acordo com o tempo do processo de fritura. Na opção "Gráficos de Score Local", os usuários podem gerar os gráficos de escores individuais, que possibilitam avaliar a distribuição das amostras para um único conjunto de dados na(s) CD(s). A única diferença desta vez é que, antes de analisar os dados, os usuários precisam selecionar na caixa "Escolha a tabela", o conjunto de dados que desejam analisar. Para fins demonstrativos, vamos considerar que almejamos verificar os escores das amostras na CD2 para o conjunto de dados de FTIR. Neste caso, os usuários precisam apertar o botão "1D", escolher a tabela "Espectros de FTIR-ATR" e, em seguida apertar o botão "Plotar". Na Figura 6Sa (Material Suplementar), temos o gráfico de escores das amostras baseados nos dados de FTIR para a CD2, com uma notável diferenciação entre as amostras de soja no quadrante superior e as de palma no inferior da CD2. A escolha da CD2 deve-se ao maior valor de saliência para o FTIR nesta CD. Concomitante à análise do gráfico de escores, é comum realizar a análise do gráfico de pesos, que é uma representação visual dos pesos atribuídos às variáveis de cada bloco para cada CD. Após apertar o botão "Loadings", os usuários precisam escolher, na caixa "Escolha a tabela", o conjunto de dados pretendido, marcar qual(is) CD(s) desejam plotar, escolher o tipo do gráfico "Discreto", "Linha" ou "Biplot" e, por fim, apertar o botão "Plotar". Para demonstração, plotaremos o gráfico de pesos para os dados de FTIR, logo, devemos escolher o conjunto de dados "Espectros de FTIR-ATR", o tipo de gráfico "Linha" e marcar as caixas da "CD2" e "Incluir intervalo ± 2 SD". Optamos novamente por incluir o gráfico de pesossomente para a CD2, pois conforme verificamos anteriormente, os dados de FTIR foram predominantes na CD2, ver Figura 6Sb. Entretanto, os usuários podem criar suas próprias opções de gráficos, incluindo ainda o gráfico biplot, análogo ao da PCA discutido anteriormente. A análise simultânea dos gráficos de escores e pesos (Figuras 6Sa e 6Sb) possibilita uma melhor interpretação dos resultados. Verificando o gráfico de escores privados para o conjunto de dados de FTIR na CD2, é possível identificar as regiões espectrais mais relevantes para a separação entre as amostras de óleo de soja e oleína de palma. De modo geral, as amostras de óleo de soja apresentaram escores positivos na CD2, com pesos predominantes na banda em ~966 cm-1, característica das ligações trans insaturadas, enquanto as amostras de oleína de palma apresentaram escores negativos, com pesos predominantes nas bandas em ~2920, ~2850, ~1465 e 1115 cm-1, todas associadas às ligações saturadas. Esses resultados destacam a capacidade discriminatória dos dados de FTIR no que diz respeito ao teor de ácidos graxos saturados e insaturados. Aprofundando a interpretação dos dados, verificamos anteriormente que o conjunto de dados que contém as informações do perfil de ácidos graxos e índice de iodo também foi predominante na CD2. Em síntese, a informação comum entre o conjunto de dados do perfil de ácidos graxos e FTIR na CD2 proporcionou uma diferenciação eficaz das amostras com base no tipo de gordura. Para mais detalhes consultar Silva et al.58 Outro recurso do GAMMA-GUI é a possiblidade de gerar o gráfico de correlação, que representa as correlações entre os escores das amostras de uma determinada CD com os valores das variáveis de um dado conjunto de dados. Apertando o botão "Correlações", os usuários podem criar seus próprios gráficos usando as opções "Discreto", "Linha", "Dispersão 2D" ou "Barras verticais". Para isso, basta escolher o conjunto de dados na caixa "Escolha a tabela", selecionar o tipo do gráfico, marcar a(s) CD(s) que se deseja avaliar e, em seguida, apertar o botão "Plotar". Antes de gerar o gráfico de correlação, os usuários podem ainda definir o valor do intervalo de confiança no nível (α) desejado. Na Figura 6Sc, apresentamos o gráfico de correlação dos escores das amostras para o conjunto de dados que correspondem ao perfil de ácidos graxos e índice de iodo, correlacionados com a CD2, CD que apresentou o maior valor de saliência para esse conjunto de dados. Esse gráfico possibilita avaliar a influência das variáveis de cada conjunto de dados. Neste caso, todas as correlações entre o conjunto de dados de perfil de ácidos graxos e índice de iodo e os escores das amostras na CD2 foram estatisticamente significativas (p < 0,05). A análise simultânea do gráfico de correlações (Figura 6Sc) e o gráfico de escores global da CD2 (Figura 6Sd) permitiu verificar que todas as amostras de óleo de soja apresentaram escores positivos na CD2, associadas a níveis mais elevados de C18:0, C18:1n9t, C18:1n7, C18:2n6c, C18:3n3, C20:0, C20:1n9, C22:0, PUFA (ácidos graxos poli-insaturados), TFA (ácidos graxos trans) e índice de iodo. Por outro lado, as amostras de palma apresentaram escores negativos na CD2, com níveis mais elevados de C12:0, C14:0, C16:0, C18:1n9c, SFA (ácido graxo saturado) e MUFA (ácido graxo monoinsaturado).58 Estatística descritiva de grupos Neste exemplo, utilizaremos um conjunto de dados composto por quatro formulações de cerveja tipo Berliner Weisse com a adição de polpa de caju, submetidas ou não ao processo de fermentação do ácido láctico. As formulações foram nomeadas como: C1 - cerveja controle, sem fermentação do ácido láctico e BW2, BW3 e BW4 - cervejas com diferentes formulações submetidas à fermentação do ácido láctico. Em todas as cervejas formuladas, foram determinados oito parâmetros físico-químicos, em triplicata: cor, pH, turbidez, diacetil, acidez, teor de álcool e ºBrix inicial e final.60 Isso resultou em uma matriz X de dimensões de 16 × 8, a qual está disponível no material de demonstração denominado "dados_cerveja" e vídeo no YouTube.61 Neste caso, desejamos verificar se existe diferença entre as formulações de cervejas com base nos parâmetros determinados. Para isso, utilizaremos a ANOVA com o teste de Tukey HSD. Na interface de "Análise Exploratória" do GAMMA-GUI, ao apertar o botão "Estatísticas de grupo", uma nova janela se abrirá. Nesta janela, os usuários devem definir os inputs para realizar a análise, inserindo a matriz de dados e os vetores que identificam as amostras e variáveis (opcional) nas seguintes caixas do aplicativo: "Matriz com os dados", "Célula contendo o grupo de cada amostra" e "Célula contendo o nome das variáveis", conforme indicado na Figura 11a. Na caixa "Estrutura de saída dos resultados" e "Alfa", os usuários podem criar suas próprias nomenclaturas ou ajustar um nível de significância (α). Entretanto, o aplicativo possui como default de saída o nome "estat_out" e o valor de alfa igual a "0.05". Após a definição das entradas dos dados, basta apertar o botão "Calcular", e então a estrutura "estat_out" será gerada no workspace do Matlab.
Dentro da estrutura de dados gerada, os usuários têm acesso à matriz de correlação, acessando "Correlação", e diversos outros resultados em "Resultados", tais como ANOVA, Tukey e letras para facilitar a comparação entre os grupos do teste de Tukey HSD. Além disso, existe uma série de outros recursos gráficos que os usuários podem utilizar, como o gráfico "Box-Plot", "Tukey HSD", "Dispersão 2D" e "Gráfico Aranha". As Figuras 11b e 11c mostram o gráfico boxplot iterativo que pode ser gerado para cada parâmetro, no qual, ao clicar sobre cada barra, é possível obter algumas métricas, como os valores de mediana, máximo, mínimo, entre outros. Além disso, há ainda o gráfico de dispersão (Figuras 11d e 11e), que permite avaliar a correlação entre os parâmetros. Outras opções de visualização compreendem os gráficos de aranha e Tukey HSD (Figura 7S, Material Suplementar). Durante a criação do gráfico de aranha (Figuras 7Sa e 7Sb), os usuários têm diversas possibilidades de personalização, como selecionar variáveis ou grupos de amostras específicas, marcando as caixas de preenchimento disponíveis na interface. Por fim, nas Figuras 7Sc e 7Sd, é mostrado o gráfico iterativo de Tukey HSD, onde os usuários podem verificar graficamente se os pares de médias em um conjunto de grupos são significativamente diferentes entre si. Tomamos como o exemplo o parâmetro "Cor", se o usuário clicar em um grupo específico na área do gráfico, verificará que o resultado fornecido no eixo x pode mudar de grupo para grupo. Neste caso, o resultado para o grupo C1 no parâmetro "Cor" indica que dois grupos possuem médias significativamente diferentes em relação a este grupo. Caso o usuário deseje ainda criar a tradicional tabela do teste de Tukey HSD, rotulando as letras para facilitar a identificação, os resultados podem ser acessados em "Grupos", dentro da estrutura "Resultados", ver Tabela 1.
CONCLUSÕES Neste tutorial, demonstramos a aplicação de cinco tipos de análise exploratória de dados (aprendizagem não supervisionada) utilizando o aplicativo GAMMA-GUI. A execução de todos os exemplos demonstrativos apresentados neste tutorial pode ser encontrado em nosso canal no YouTube®. O aplicativo GAMMA-GUI está disponibilizado para download gratuito no File Exchange - MATLAB Central ou no GitHub®, contando com uma interface gráfica amigável, desenvolvida em GUI (Graphical User Interface) e implementada usando programação orientada a objetos (object-oriented programming, OOP) no software Matlab®. O aplicativo permite que usuários novatos e experientes realizem tarefas de forma eficaz e eficiente sem a necessidade de conhecimentos prévios em linguagem de programação. No entanto, é importante ressaltar que, para utilizar o aplicativo com eficiência, é recomendável que os usuários possuam conhecimentos básicos em quimiometria. Em nossa série de artigos tutoriais publicados na revista Química Nova,17 estamos explorando diferentes recursos do aplicativo GAMMA-GUI. Nos próximos tutoriais, focaremos nos recursos de análises de dados disponíveis nas interfaces de "Calibração" e "Classificação" multivariada.
MATERIAL SUPLEMENTAR O material suplementar deste trabalho encontra-se disponível no site http://quimicanova.sbq.org.br/, em arquivo PDF, com acesso gratuito.
DECLARAÇÃO DE DISPONIBILIDADE DE DADOS Os dados estão disponibilizados em: https://github.com/appGAMMA/GAMMA-GUI_aplicativo.
AGRADECIMENTOS Os autores agradecem aos usuários do aplicativo por todas as contribuições, sugestões de melhorias e ideias de implementação fornecidas. Agradecemos também aos órgãos de fomento à pesquisa: CNPq (processos 312595/2021-2 e 142038/2024-5).
CONTRIBUIÇÕES DO AUTOR Diego Galvan: conceituação, curadoria de dados, análise formal, software, validação, visualização, redação de rascunho original e redação-revisão e edição; Tácito Lucena Conte: investigação, recursos, software, validação, visualização, redação de rascunho original e redação-revisão e edição; João Marcos Marques Liduário: investigação, recursos, software, validação, visualização, redação de rascunho original e redação-revisão e edição; Jelmir Craveiro de Andrade: investigação, recursos, software, validação, visualização, redação de rascunho original e redação-revisão e edição; Patrícia Casarin: investigação, recursos, software, validação, visualização, redação de rascunho original e redação-revisão e edição; Evandro Bona: conceituação, curadoria de dados, aquisição de financiamento, investigação, administração de projetos, recursos, software, validação, visualização, redação de rascunho original e redação-revisão e edição.
REFERÊNCIAS 1. Varmuza, K.; Filzmoser, P.; Introduction to Multivariate Statistical Analysis in Chemometrics; CRC press: Boca Raton, EUA, 2016. 2. Kowalski, B. R.; J. Chem. Inf. Comput. Sci. 1975, 15, 201. [Crossref] 3. Ferreira, M. M. C.; Quimiometria - Conceitos Métodos e Aplicações Unicamp: Campinas, 2015. 4. Galvan, D.; de Aguiar, L. M.; Bona, E.; Marini, F.; Killner, M. H. M.; Anal. Chim. Acta 2023, 1273, 341495. [Crossref] 5. Martinez, W. L.; Martinez, A. R.; Solka, J.; Exploratory Data Analysis with MATLAB; CRC Press: New York, EUA, 2017. 6. Brereton, R. G.; Chemometrics for Pattern Recognition; John Wiley & Sons: Bristol, UK, 2009. 7. dos Santos, D. P.; Sena, M. M.; Almeida, M. R.; Mazali, I. O.; Olivieri, A. C.; Villa, J. E. L.; Anal. Bioanal. Chem. 2023, 415, 3945. [Crossref] 8. Chiappini, F. A.; Goicoechea, H. C.; Olivieri, A. C.; Chemom. Intell. Lab. Syst. 2020, 206, 104162. [Crossref] 9. Olivieri, A. C.; Wu, H.-L.; Yu, R.-Q.; Chemom. Intell. Lab. Syst. 2009, 96, 246. [Crossref] 10. Olivieri, A. C.; Wu, H.-L.; Yu, R.-Q.; Chemom. Intell. Lab. Syst. 2012, 116, 9. [Crossref] 11. Zontov, Y. V.; Rodionova, O. Y.; Kucheryavskiy, S. V.; Pomerantsev, A. L.; Chemom. Intell. Lab. Syst. 2017, 167, 23. [Crossref] 12. Zontov, Y. V.; Rodionova, O. Y.; Kucheryavskiy, S. V.; Pomerantsev, A. L.; Chemom. Intell. Lab. Syst. 2020, 203, 104064. [Crossref] 13. Jaumot, J.; de Juan, A.; Tauler, R.; Chemom. Intell. Lab. Syst. 2015, 140, 1. [Crossref] 14. Helfer, G. A.; Bock, F.; Marder, L.; Furtado, J. C.; da Costa, A. B.; Ferrão, M. F.; Quim. Nova 2015, 38, 575. [Crossref] 15. Siqueira, B. M. M.; Silva, A. L. S.; Folli, G. S.; Rosa, T. R.; Romão, W.; Lelis, M. F. F.; Filgueiras, P. R.; Moura, P. R. G.; Quim. Nova 2024, 47, e-20230138. [Crossref] 16. Helfer, G. A.; Magnus, V. S.; Böck, F. C.; Teichmann, A.; Ferrão, M. F.; da Costa, A. B.; J. Braz. Chem. Soc. 2017, 28, 328. [Crossref] 17. Galvan, D.; Bona, E.; Quim. Nova 2024, 47, e-20240005. [Crossref] 18. Canal YouTube, Aplicativo GAMMA | Análise Multivariada, https://www.youtube.com/@appGAMMA, acessado em agosto 2025. 19. File Exchange MathWorks, GAMMA, https://www.mathworks.com/matlabcentral/fileexchange/156857-gamma, acessado em agosto 2025. 20. appGAMMA / GAMMA-GUI_aplicativo, https://github.com/appGAMMA/GAMMA-GUI_aplicativo, acessado em agosto 2025. 21. Mazivila, S. J.; Olivieri, A. C.; TrAC, Trends Anal. Chem. 2018, 108, 74. [Crossref] 22. Pomerantsev, A. L.; Chemometrics in Excel; John Wiley & Sons: New Jersey, EUA, 2014. 23. de Souza, A. M.; Poppi, R. J.; Quim. Nova 2012, 35, 223. [Crossref] 24. Olivieri, A. C.; Introduction to Multivariate Calibration; Springer International Publishing: Cham, Switzerland, 2018. 25. Bro, R.; Smilde, A. K.; Anal. Methods 2014, 6, 2812. [Crossref] 26. Rodionova, O.; Kucheryavskiy, S.; Pomerantsev, A.; Chemom. Intell. Lab. Syst. 2021, 213, 104304. [Crossref] 27. Kohonen, T.; Self-Organizing Maps; Springer: Berlin, Heidelberg, 2001. [Crossref] 28. Haykin, S.; Neural Networks and Learning Machines; Pearson Education India: New Jersey, EUA, 2009. 29. Matlab Software, The MathWorks Inc., linkage, https://www.mathworks.com/help/stats/linkage.html, acessado em agosto 2025. 30. Ferreira, M. M. C.; Quim. Nova 2022, 45, 1251. [Crossref] 31. Matlab Software, The MathWorks Inc., pdist, https://www.mathworks.com/help/stats/pdist.html, acessado em agosto 2025. 32. Bishop, C. M.; Pattern Recognition and Machine Learning; Springer: New York, EUA, 2006. 33. Qannari, E. M.; Wakeling, I.; Courcoux, P.; MacFie, H. J. H.; Food Quality and Preference 2000, 11, 151. [Crossref] 34. Galvan, D.; de Andrade, J. C.; Conte-Junior, C. A.; Killner, M. H. M.; Bona, E.; Chemom. Intell. Lab. Syst. 2023, 233, 104748. [Crossref] 35. Bouveresse, D. J.-R.; Rutledge, D. N.; J. Chemom. 2024, 38, e3454. [Crossref] 36. Mishra, P.; Roger, J. M.; Rutledge, D. N.; Biancolillo, A.; Marini, F.; Nordon, A.; Jouan-Rimbaud-Bouveresse, D.; Chemom. Intell. Lab. Syst. 2020, 205, 104139. [Crossref] 37. Cariou, V.; Bouveresse, D. J.-R.; Qannari, E. M.; Rutledge, D. N.; Em Data Fusion Methodology and Applications; Cocchi, M., org.; Elsevier, 2019. 38. El Ghaziri, A.; Cariou, V.; Rutledge, D. N.; Qannari, E. M.; J. Chemom. 2016, 30, 420. [Crossref] 39. de Aguiar, L. M.; Galvan, D.; Bona, E.; Colnago, L. A.; Killner, M. H. M.; Talanta 2022, 236, 122838. [Crossref] 40. Hair, J. F.; Black, W. C.; Babin, B. J.; Anderson, R. E.; Tatham, R. L.; Análise Multivariada de Dados; Bookman Editora: Porto Alegre, Brasil, 2009. 41. YouTube, Instalação do GAMMA-GUI pelo File Exchange, https://www.youtube.com/watch?v=3QP9WdyQqOA, acessado em agosto 2025. 42. MATLAB for Artificial Intelligence, https://www.mathworks.com/, acessado em agosto 2025. 43. Instagram, Sabia que é Possível Usar o Matlab sem Custo? Siga as Dicas e Explore o GAMMA, https://www.instagram.com/p/C-5_IsjxAX4/, acessado em agosto 2025. 44. Forina, M.; Armanino, C.; Castino, M.; Ubigli, M.; Vitis 1986, 25, 189. [Crossref] 45. YouTube, Demonstração 9 - Análise de Componentes Principais (PCA) no GAMMA-GUI, https://www.youtube.com/watch?v=-iBHnG1e7H4&t=13s, acessado em agosto 2025. 46. Savorani, F.; Tomasi, G.; Engelsen, S. B.; J. Magn. Reson. 2010, 202, 190. [Crossref] 47. Chemometrics Research, www.models.life.ku.dk, acessado em agosto 2025. 48. Gemperline, P.; Practical Guide to Chemometrics; CRC Press: Boca Raton, EUA, 2006. 49. Fisher, R. A.; Annals of Eugenics 1936, 7, 179. [Crossref] 50. YouTube, Demonstração 10 - Mapas Auto-Organizáveis (SOM) no GAMMA-GUI, https://www.youtube.com/watch?v=bfYyuOT-XQU, acessado em agosto 2025. 51. Haykin, S.; Redes Neurais: Princípios e Prática; Bookman Editora: Porto Alegre, Brasil, 2007. 52. Gorban, A. N.; Sumner, N. R.; Zinovyev, A. Y.; Applied Mathematics Letters 2007, 20, 382. [Crossref] 53. Cremasco, H.; Borsato, D.; Angilelli, K. G.; Galão, O. F.; Bona, E.; Valle, M. E.; J. Sci. Food Agric. 2016, 96, 306. [Crossref] 54. Galvan, D.; Effting, L.; Torres Neto, L.; Conte-Junior, C. A.; Compr. Rev. Food Sci. Food Saf. 2021, 20, 3136. [Crossref] 55. YouTube, Demonstração 11 - Análise de Agrupamentos por Métodos Hierárquicos (HCA) no GAMMA-GUI, https://www.youtube.com/watch?v=rCeE-6Sjqpo, acessado em agosto 2025. 56. Galvan, D.; Lelis, C. A.; Effting, L.; Melquiades, F. L.; Bona, E.; Conte-Junior, C. A.; Microchem. J. 2022, 181, 107746. [Crossref] 57. YouTube, Demonstração 12 - Agrupamento k-means no GAMMA-GUI, https://www.youtube.com/watch?v=b_6th7pHFDs, acessado em agosto 2025. 58. Silva, J. A.; Dorocz, E. L.; Sanchez, J. L.; dos Santos, L. D.; Beneti, S. C.; Tanamati, A.; Bona, E.; Tanamati, A. A. C.; J. Food Compos. Anal. 2024, 126, 105897. [Crossref] 59. YouTube, Demonstração 13 - Método de Análise por Dimensões Comuns (ComDim) no GAMMA-GUI, https://www.youtube.com/watch?v=N2DAXdESvCc, acessado em agosto 2025. 60. Alberti, M. L.; Mascareli, V. A. B.; Galvan, D.; Costa, G. A. N.; Guergoletto, K. B.; Spinosa, W.; Semina: Cienc. Agrar. 2023, 44, 1341. [Crossref] 61. YouTube, Demonstração 14 - Estatística de grupos no GAMMA-GUI, https://www.youtube.com/watch?v=gQ7_n-8uBmU&t=4s, acessado em agosto 2025.
#Grupo de Análise Multivariada em Matrizes Alimentares (GAMMA) |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access







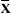 (I × J) pré-tratada, geralmente centrada na média ou autoescalada produz uma matriz de escores T (I × A, com colunas mutuamente ortogonais), uma de pesos L (J × A,
com colunas ortonormais, ou seja, não correlacionadas) e uma de resíduos E (I × J, com informação não modelada), sendo A a quantidade de PCs consideradas na análise (Equação 1).
(I × J) pré-tratada, geralmente centrada na média ou autoescalada produz uma matriz de escores T (I × A, com colunas mutuamente ortogonais), uma de pesos L (J × A,
com colunas ortonormais, ou seja, não correlacionadas) e uma de resíduos E (I × J, com informação não modelada), sendo A a quantidade de PCs consideradas na análise (Equação 1).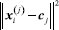 , é o quadrado da distância Euclidiana entre um objeto
, é o quadrado da distância Euclidiana entre um objeto 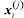 do cluster j e centroide do cluster cj. Outras métricas para estimativas das distâncias podem ser usadas, bem como diferentes algoritmos têm sido propostos para minimizar a função objetivo.1 Ao avaliar a matriz de dados X com k-means, é necessário inicialmente a definição de uma quantidade k de clusters inerentes ao conjunto de dados, que geralmente é desconhecido. Como a modelagem é muito rápida, ela pode ser executada para uma variedade de números diferentes de clusters, e consequentemente o melhor resultado pode ser selecionado.1,28,32 Apesar da necessidade de definir um número inicial de clusters, o k-means é considerado um algoritmo de aprendizado não supervisionado, pois não depende de dados de entrada rotulados para treinamento. Ele apenas organiza os dados em clusters com base em similaridades inerentes, sem qualquer rótulo predefinido.1
do cluster j e centroide do cluster cj. Outras métricas para estimativas das distâncias podem ser usadas, bem como diferentes algoritmos têm sido propostos para minimizar a função objetivo.1 Ao avaliar a matriz de dados X com k-means, é necessário inicialmente a definição de uma quantidade k de clusters inerentes ao conjunto de dados, que geralmente é desconhecido. Como a modelagem é muito rápida, ela pode ser executada para uma variedade de números diferentes de clusters, e consequentemente o melhor resultado pode ser selecionado.1,28,32 Apesar da necessidade de definir um número inicial de clusters, o k-means é considerado um algoritmo de aprendizado não supervisionado, pois não depende de dados de entrada rotulados para treinamento. Ele apenas organiza os dados em clusters com base em similaridades inerentes, sem qualquer rótulo predefinido.1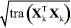 , a fim de garantir a mesma variância total entre os blocos. A função tra (⋅) ou traço, representa a soma dos elementos da diagonal principal de uma matriz quadrada. No contexto da norma de Frobenius, utiliza-se o traço de XTX, onde X é uma matriz de dimensão J × J. O produto XTX resulta em uma matriz quadrada de dimensão J × J. O traço de XTX, nesse caso, equivale à soma dos quadrados de todos os elementos da matriz X. Essa normalização é especialmente importante no ComDim, pois assegura que todas as matrizes de entrada tenham a mesma variância total, impedindo que uma matriz com maior escala ou amplitude domine a análise. Q é a matriz ortonormal cujas colunas correspondem aos vetores de escores q1, q2, ..., qA, representando as dimensões comuns (do inglês common dimensions, CDs) extraídas. Λk é uma matriz diagonal cujos elementos λ1(k), λ2(k), ..., λA(K) indicam a saliência (ou peso) da matriz Xk para cadadimensão comum a. Finalmente, Ek representa a matriz residual associada à decomposição de Wk, ou seja, a parte que não é explicada pelas CDs. Uma fundamentação teórica mais detalhada do ComDim pode ser encontrada em Qannari et al.,33 Galvan et al.34 e Bouveresse e Rutledge.35
, a fim de garantir a mesma variância total entre os blocos. A função tra (⋅) ou traço, representa a soma dos elementos da diagonal principal de uma matriz quadrada. No contexto da norma de Frobenius, utiliza-se o traço de XTX, onde X é uma matriz de dimensão J × J. O produto XTX resulta em uma matriz quadrada de dimensão J × J. O traço de XTX, nesse caso, equivale à soma dos quadrados de todos os elementos da matriz X. Essa normalização é especialmente importante no ComDim, pois assegura que todas as matrizes de entrada tenham a mesma variância total, impedindo que uma matriz com maior escala ou amplitude domine a análise. Q é a matriz ortonormal cujas colunas correspondem aos vetores de escores q1, q2, ..., qA, representando as dimensões comuns (do inglês common dimensions, CDs) extraídas. Λk é uma matriz diagonal cujos elementos λ1(k), λ2(k), ..., λA(K) indicam a saliência (ou peso) da matriz Xk para cadadimensão comum a. Finalmente, Ek representa a matriz residual associada à decomposição de Wk, ou seja, a parte que não é explicada pelas CDs. Uma fundamentação teórica mais detalhada do ComDim pode ser encontrada em Qannari et al.,33 Galvan et al.34 e Bouveresse e Rutledge.35